決定木（Decision tree）：様々なアルゴリズム

前回は、決定木（decision tree）の基本的な概念について説明しました。前回の最後のところで触れたように、decision treeは複数組み合わせることによってより良いモデルになる可能性があります。そこで今回は、Boosting (AdaBoost), Bagging, Random Forest, Gradient Boostingといった、複数のtreeを組み合わせて一つのモデルを作り上げる方法について解説したいと思います。

モデル作成の目標は前回と同じ、

というものです。

※前回と同様、pythonのコードを併用して説明します。セットアップに必要なコードについても、前回の記事をご覧ください。

Boosting

“Boosting”では、モデルを何回も反復して作成し、毎回そのエラーに注目し、それを元に次々とtreeを作成していく方法です。

まず初めにデータを用いてtreeを1つ作成します。次に、そのtreeによって間違って分類したサンプルにweightを置き、これらをできる限り正確にクラス分けすることを優先したtreeを作成します（もちろん、それによって他のサンプルのmisclassificationが起こる可能性はあります）。

# モデルの作成
clf = tree.DecisionTreeClassifier(max_depth=1)
mdl = ensemble.AdaBoostClassifier(base_estimator=clf,n_estimators=6)
mdl = mdl.fit(X_train,y_train)

# 図の作成
fig = plt.figure(figsize=[12,6])
for i, estimator in enumerate(mdl.estimators_):
    ax = fig.add_subplot(2,3,i+1)
    txt = 'Tree {}'.format(i+1)
    dtn.plot_model_pred_2d(estimator, X_train, y_train, title=txt)

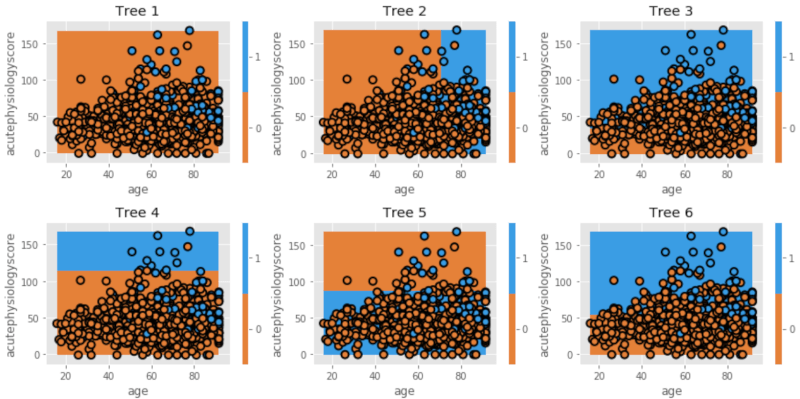
初めのモデル（Tree 1）はweightを置いていないため、前回の記事で作成した最初のモデル（比較のため、splitは1つだけのtreeを作成）と同じになっています。次のモデル（Tree 2）では、初めのモデルで間違って分類したサンプルのクラス分けにweightを置き、かつ残りのデータもできる限り正確に分類できる境界線を引きます。そして次は、Tree 2で間違って分類したサンプルに新たにweightを加え、最適な境界線を新たに作成します（Tree 3）。。。この操作を何度も繰り返し（iteration）、境界線が分けることのできるサンプルが少なくなるまで行います。

最後にこれらのtreeを組み合わせて最終モデルを作りますが、それぞれのtreeによるエラー（misclassificationの総数）によって最終モデルへの貢献度が異なります。例えば、上記の例ではTree 1はTree 6よりも全体のエラーが少ないので、最終モデルへの関与（weight）は大きくなります。これが”AdaBoost（Adaptive Boosting）“というアルゴリズムの基本的な概念です。

今回の最終モデルは、以下のように図示されます。

plt.figure(figsize=[9,5])
txt = 'Boosted tree (final decision surface)'
dtn.plot_model_pred_2d(mdl, X_train, y_train, title=txt)

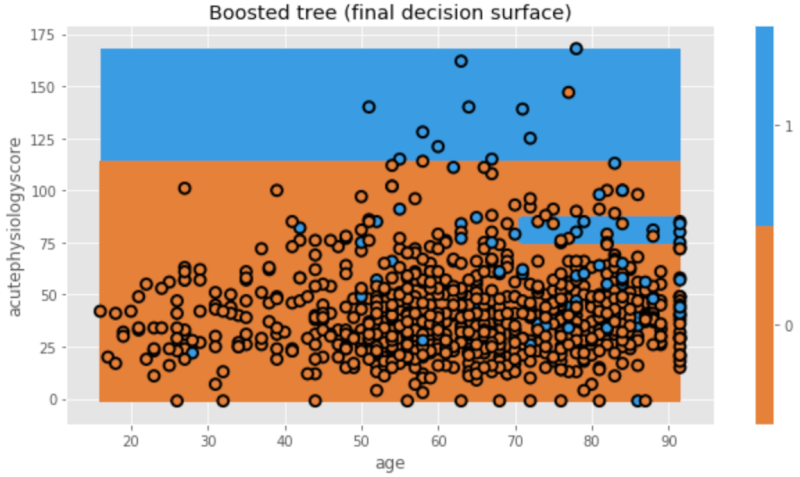
Bagging

“Boostrap aggegation”や”Bagging”と呼ばれる方法も、幾つかのモデルを組み合わせて一つの良いモデルを作り上げるという点ではAdaBoostと同じです。

AdaBoostでは、[A,B,C]という三つのサンプルがあり、Cを間違って分類したとします。AdaBoostの新しいtreeではこのCに重みを与えてモデルを作り直します。これは、Cというサンプルを意図的に何回もデータセットに組み込み（ex. [A,B,C,C,C]）、Cを他のサンプルよりも重要視するような新しいモデルを作っている、と言い換えることもできます。

一方、Boostrap aggegation/Baggingでは、AdaBoostのような意図的なサンプルの抽出（C）は行わず、トレーニングセットから毎回ランダムにデータセットを取り出します（resampling）。そして、それぞれ独立したデータセットを元にtreeを作り、最後に組み合わせて一つのモデルを作り上げます。

以下は、boostrapを用いてtreeを6個作った場合です。

# モデルの作成
clf = tree.DecisionTreeClassifier(max_depth=5)
mdl = ensemble.BaggingClassifier(base_estimator=clf, n_estimators=6)
mdl = mdl.fit(X_train, y_train)

# 図の作成
fig = plt.figure(figsize=[12,6])
for i, estimator in enumerate(mdl.estimators_):    
    ax = fig.add_subplot(2,3,i+1)
    txt = 'Tree {}'.format(i+1)
    dtn.plot_model_pred_2d(estimator, X_train, y_train, 
                           title=txt)

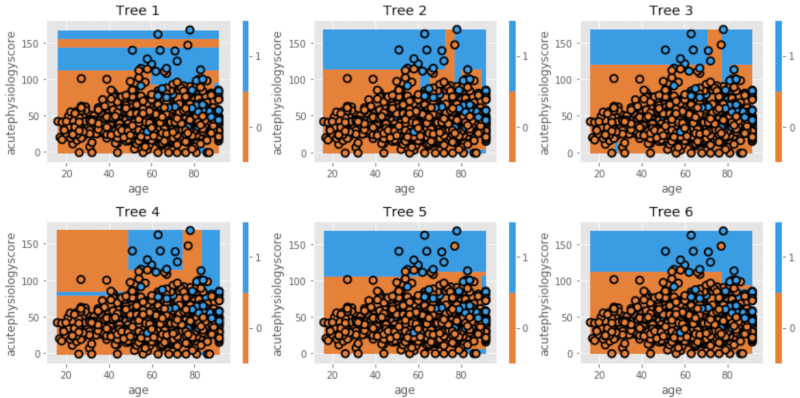
個々のtreeはそれぞれ異なっていますね。これは、モデル作りに際し毎回ランダムにデータセットを作っているからです。最終モデルとしてこれらを組み合わせると、以下のようになります。

plt.figure(figsize=[8,5])
txt = 'Bagged tree (final decision surface)'
dtn.plot_model_pred_2d(mdl, X_train, y_train, title=txt)

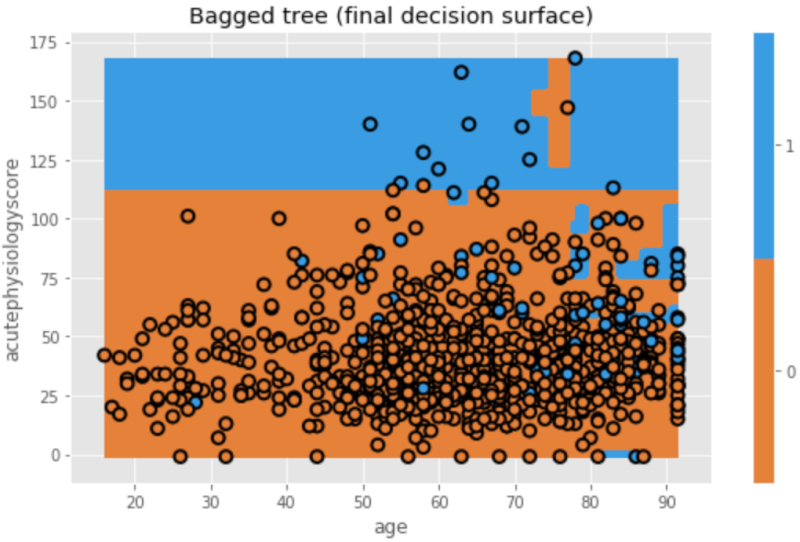
Random Forest

Random forestでは、baggingと同様ランダムにデータセットを取り出す（resampling）と同時に、毎回ランダムに選んだ一部の予測因子のみを用いてtreeを作り、最後にそれらを組み合わせます。時に必要な、時に不要な予測因子が選択される場合があり、一つ一つのtreeの違い（variance）は大きくなりますが、splitに用いられる予測因子がランダムに選ばれるため、それらのtreeをまとめた最終モデルのvarianceとbiasは小さくなります。

では、Random Forestによりtreeを作ってみましょう。

# モデルの作成
mdl = ensemble.RandomForestClassifier(max_depth=5, n_estimators=6, max_features=1)
mdl = mdl.fit(X_train,y_train)

# 図の作成
fig = plt.figure(figsize=[12,6])
for i, estimator in enumerate(mdl.estimators_):    
    ax = fig.add_subplot(2,3,i+1)
    txt = 'Tree {}'.format(i+1)
    dtn.plot_model_pred_2d(estimator, X_train, y_train, title=txt)

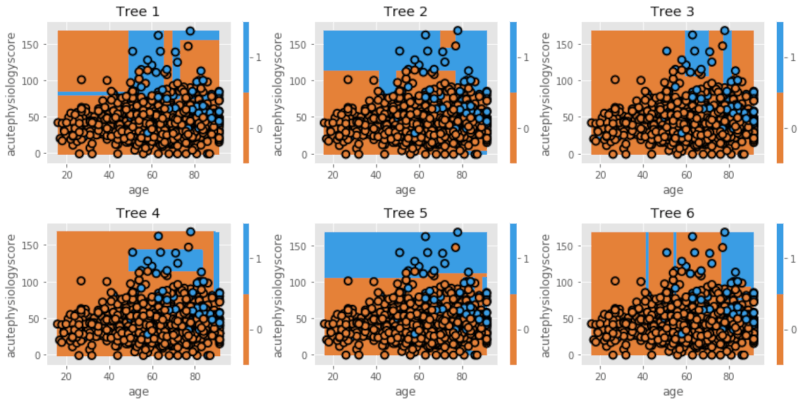
これを合わせた最終モデルが下のようになります。

plt.figure(figsize=[9,5])
txt = 'Random forest (final decision surface)'
dtn.plot_model_pred_2d(mdl, X_train, y_train, title=txt)

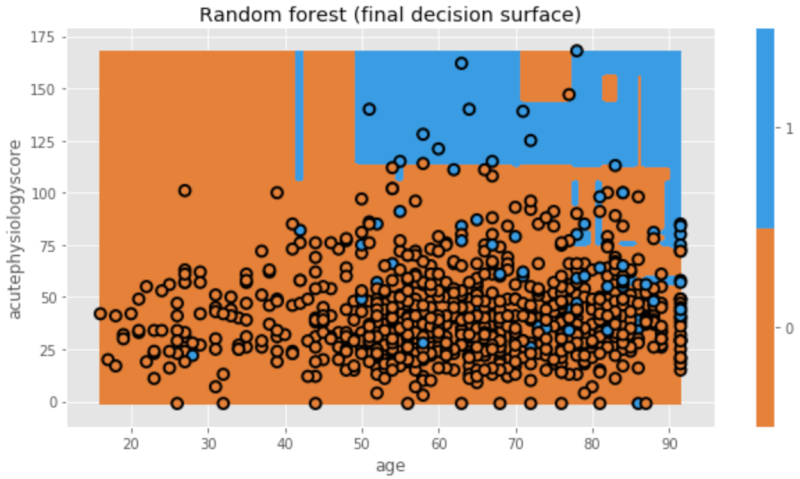
Gradient Boosting

Gradient boostingは、misclassificationを減らすため前のtreeを考慮するというboostingの概念と、一部の予測因子をランダムに用いてoverfittingを減らすというRandom Forestの概念を組み合わせたものです。

詳細は割愛しますが、簡単に表現するならばGradient boostingはboosting modelを数学的に捉えることになります。Treeがどの程度良いものでどの程度複雑であるかを、数学的な”function”を用いて判断しtreeを作成します。

# モデルの作成
mdl = ensemble.GradientBoostingClassifier(n_estimators=10)
mdl = mdl.fit(X_train, y_train)

# 図の作成
plt.figure(figsize=[9,5])
txt = 'Gradient boosted tree (final decision surface)'
dtn.plot_model_pred_2d(mdl, X_train, y_train, title=txt)

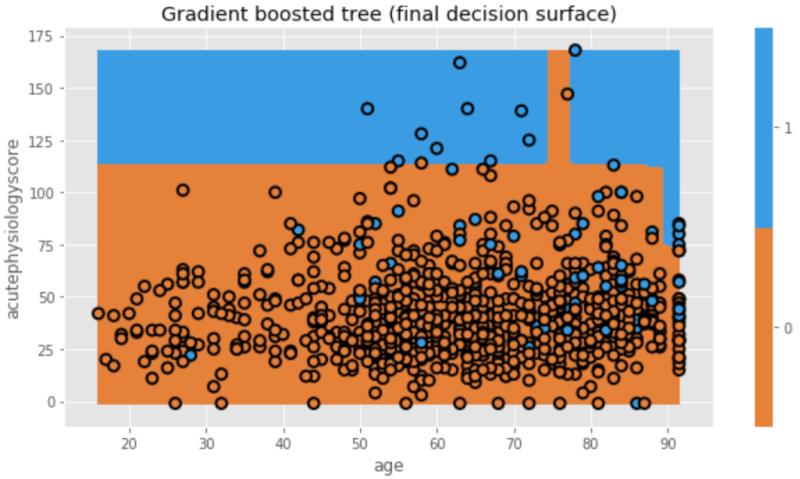
Model performanceの比較

最後に、これまで説明してきた様々なモデルのパフォーマンスを、テストセットを用いて比べてみましょう。要するに、ICU入室初日の年齢と重症度スコアという二つの予測因子によって、院内死亡がどのくらい正確に予測できるかを、これまで解説した様々なモデルの間で比べてみます。

clf = dict()
clf['Decision Tree'] = tree.DecisionTreeClassifier(criterion='entropy', splitter='best').fit(X_train,y_train)
clf['Gradient Boosting'] = ensemble.GradientBoostingClassifier(n_estimators=10).fit(X_train, y_train)
clf['Random Forest'] = ensemble.RandomForestClassifier(n_estimators=10).fit(X_train, y_train)
clf['Bagging'] =  ensemble.BaggingClassifier(n_estimators=10).fit(X_train, y_train)
clf['AdaBoost'] =  ensemble.AdaBoostClassifier(n_estimators=10).fit(X_train, y_train)

fig = plt.figure(figsize=[10,10])

print('AUROC\tModel')
for i, curr_mdl in enumerate(clf):    
    yhat = clf[curr_mdl].predict_proba(X_test)[:,1]
    score = metrics.roc_auc_score(y_test, yhat)
    print('{:0.3f}\t{}'.format(score, curr_mdl))
    ax = fig.add_subplot(3,2,i+1)
    dtn. plot_model_pred_2d(clf[curr_mdl], X_test, y_test, title=curr_mdl)

すると、このような結果を得ることができました。

AUROC	Model
0.593	Decision Tree
0.782	Gradient Boosting
0.692	Random Forest
0.685	Bagging
0.759	AdaBoost

 

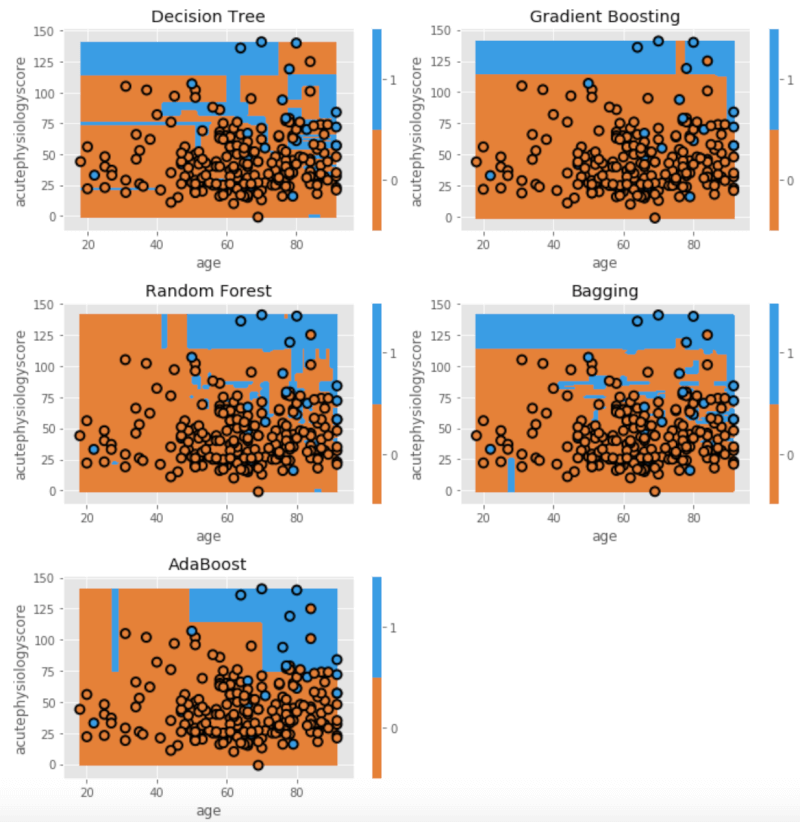
今回は、定量的にGradient Boostingが最も正確にアウトカム（生死）を区別できることを示しています。ちなみに、一般的にはシンプルな境界線を持つモデルの方が、テストセットへの一般化が有利にある傾向があります。

まとめ

前回と今回、2回に分けて決定木（decision tree）を元にした様々な機械学習（machine learning）の、基本的な概念や方法を解説しました。少しでも理解の助けになれば幸いです。

 

⇒医療従事者に必要な統計学と疫学（目次）へ

参考文献

1. Tom Pollard. HST 953. Prediction and Classification Tree. Massachusetts Institute of Technology.
2. Nancy Cook and Fran Cook. EPI 288. Data Mining. Harvard T.H. Chan School of Public Health
3. Gareth James et al. “An Introduction to Statistical Learning” with Application s in R.