生存解析をする上で欠かせない”Kaplan-Meier（カプランマイヤー）”。もはやその方法（Kaplan-Meier estimator）を用いるのに、元文献を提示しなくても良いほどメジャーなものになりました。今回は、そのKaplan-Meierの理屈をRとともに解説したいと思います。
内容
Censoringのない場合
観察期間中のdrop-out（”loss to follow-up”）や観察期間中のeventなし（”administrative censoring”）といったcensoringがない場合は、すべての患者において観察期間中にeventが発生したことになります。
求めたいゴールであるS(t)は、eventまでの期間がtより長くなる確率（ex. tより長く生存する確率）です。S(8)であれば、8 weeksより後にeventが起こる確率であす。今回の例では計21人中、青字で示した8人となる確率、すなわち、P(T>8) = 8/21 = 0.381となります。Censoringがなければ、どのタイミングであっても分母はtotal数の21であり、すべてのS(t)を簡単に求められます。
（すなわち、Kaplan-Meierを用いるまでもありません）
手計算で簡単に求められますが、折角なのでRを使ってみましょう。survivalというpackageを用います。
|
1 2 3 4 |
library(survival) t<-c(1, 1, 2, 2, 3, 4, 4, 5, 5, 8, 8, 8, 8, 11, 11, 12, 12, 15,17, 22, 23) km<-survfit(Surv(t, rep(1,21))~1) summary(km) |
とすると、アウトプットは以下のようになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
## time n.risk n.event survival std.err lower 95% CI upper 95% CI ## 1 21 2 0.9048 0.0641 0.78754 1.000 ## 2 19 2 0.8095 0.0857 0.65785 0.996 ## 3 17 1 0.7619 0.0929 0.59988 0.968 ## 4 16 2 0.6667 0.1029 0.49268 0.902 ## 5 14 2 0.5714 0.1080 0.39455 0.828 ## 8 12 4 0.3810 0.1060 0.22085 0.657 ## 11 8 2 0.2857 0.0986 0.14529 0.562 ## 12 6 2 0.1905 0.0857 0.07887 0.460 ## 15 4 1 0.1429 0.0764 0.05011 0.407 ## 17 3 1 0.0952 0.0641 0.02549 0.356 ## 22 2 1 0.0476 0.0465 0.00703 0.322 ## 23 1 1 0.0000 NaN NA NA |
t=8の時のsurvival probabilityは0.381となっていますね。
Censoringのある場合
まずは用語の説明をします。生存解析においては、censoringとなった人には、その時点の時間の横に”+”を付けて表します。10週でloss to follow-upとなれば、”10+”と記します。
そして、tjを時点j, djを時点jにおけるevent発生数, cjを時点jにおけるcensorとなった人数として、それぞれ表します。
censoringがある場合、S(t)の計算は上記のように単純にはいきません。なぜなら、censoringとなった人が、どのタイミングでeventが起こったかわからないから、すなわち、分母が必ずしもトータル人数になりません。
そこで、Kaplan-Meierという方法を用いてS(t)を推測することになります。
Kaplan-Meier Estimator
tが連続ではなく時点・時点で区切られている（Day1, Day2…など）discrete caseを考えてみましょう。
詳細は上記のような数式から導かれますが、S(t) = P(T > t)は結局は、
それぞれの時点での［1 – ｛eventが起こった人数（dj）/リスクのある人数（rj）｝］を、時点jまで掛け合わせたもの
になります。といってもわかりにくいですよね。Kaplan-Meierは、一度自分で表を作ることをお勧めします。それぞれの時点tjにおける、dj, cj, rjを書き、そこから1-dj/rj、そしてS(tj)を計算します。
上記の例を表にすると、以下のようになります。
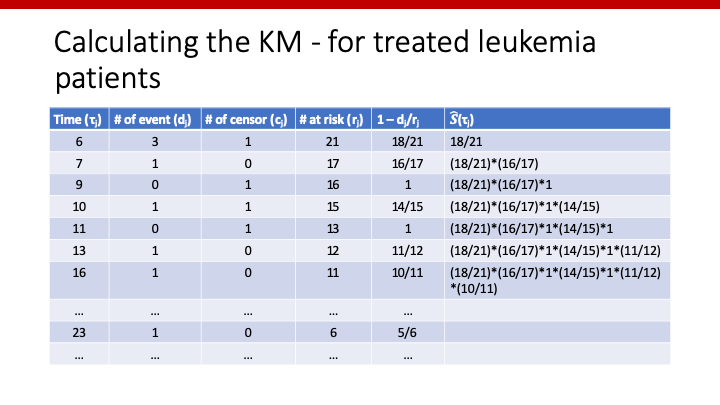
この一番右列にあるS(t)が、Kaplan-Meier estimatorを用いて推測したS(t)です。Kaplan-Meierも、ちゃんと手計算できますね。
こちらも、Rを用いて算出してみましょう。
|
1 2 3 4 5 |
c1<-data.frame(time=c(6,6,6,6,7,9,10,10,11,13,16,17,19,20,22,23,25,32,32,34,35)) c2<-data.frame(remission=c(0,1,1,1,1,0,0, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0)) dat<-cbind(c1,c2) km<-survfit(Surv(time, remission)~1, data=dat) summary(km) |
アウトプットは、以下のようになります。
|
1 2 3 4 5 6 7 8 |
## time n.risk n.event survival std.err lower 95% CI upper 95% CI ## 6 21 3 0.857 0.0764 0.720 1.000 ## 7 17 1 0.807 0.0869 0.653 0.996 ## 10 15 1 0.753 0.0963 0.586 0.968 ## 13 12 1 0.690 0.1068 0.510 0.935 ## 16 11 1 0.627 0.1141 0.439 0.896 ## 22 7 1 0.538 0.1282 0.337 0.858 ## 23 6 1 0.448 0.1346 0.249 0.807 |
いかがでしょうか。手計算と同じS(t)が得られたでしょうか。
計算してみればわかりますが、censoringがない場合もKaplan-Meierを使うことができ、上記と同じ結果になります。
Kaplan-Meierの生存曲線
最後に、Kaplan-Meier Estimatorを用いた生存曲線を描いてみましょう。縦軸にS(t)、横軸に時間をとります。上の手計算で作成した表を元に描くことができますが、ここではRを使って描いてみましょう。先ほど定義したkmを用います。
|
1 |
plot(km, ylab="Survival probability S(t)", xlab="Time (weeks)", main="Kaplan-Meier", conf.int=F, mark.time=T,cex=0.5) |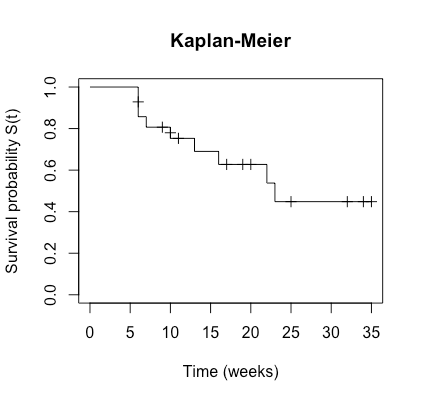
ちゃんとKaplan-Meierの生存曲線が描けました。ちなみに、生存曲線と直交している短い線は、censoringの患者を表しています。
まとめ
Kaplan-Meierを理解するためには、上記のような表を一度でいいから自分で作ることがとても重要です。Event発生だけでなく、それが起こるまでの時間にも興味がある、途中でfollow-upできなくなりoutcomeがわからない人がいる、といった場合には、視覚的にも有効な方法ですので、是非理解しておいてください。
Reference
Andrea Bellavia. BST 223: Applied Survival Analysis. Harvard T.H. Chan School of Public Health
私はブラウンでMPH、ワシントン大学の疫学博士課程にいます。（現在アラフォー独身女性w、私の専門分野であるインドの伝統医学の研究のために進学しました。KーMとてもわかりやすかった上にRのコードまでついていてとてもありがたかったです！これからもこのような情報とてもお待ちしています！！