実際のデータを扱う際、ほぼ確実に欠損値(missing value)というものが存在します。全てのデータが完全に揃っているということは、扱うデータが大きければ大きいほど非現実的となります。
では、欠損値がある場合、単にそのデータを除いて解析しても良いのでしょうか。答えはYes and Noです。どういう時に良いのか、どういう場合にダメなのかを理解するためには、欠損値の種類について理解しなければなりません。今回は、欠損値の分類について解説したいと思います。
欠損値によって引き起こされる問題
データベースに欠損値があると、関連性を見る際に統計学的な問題が発生することがあります。まずは、その例を挙げてみましょう。Quality of Life (QOL)を半年毎に調べたデータを考えてみます。
①欠損値がない場合
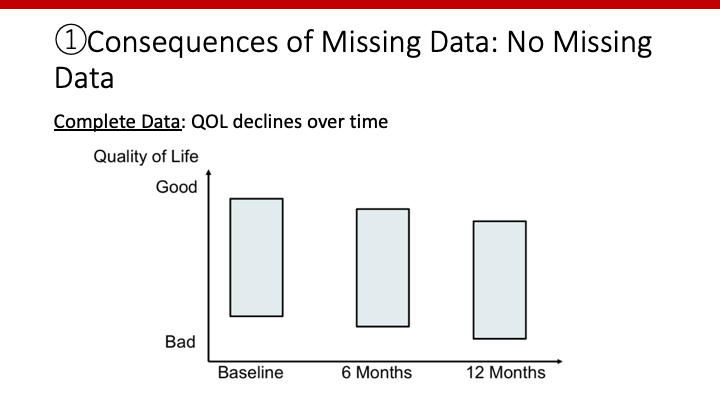
上は欠損値のない場合です。個々で少しずつQOLが異なりますので、そのデータの広がりを縦の広がりとして表しています。
欠損値がない場合は、半年毎にQOLが低下していることがわかります。平均値や中央値で考えるとわかりやすいですね。Baseline、6ヶ月後、12ヶ月後で、それぞれの真ん中は徐々に下がってきています。完全なデータであるので、これが知りたい本当の変化だとします。
②アウトカムと関係しない欠損値がある場合
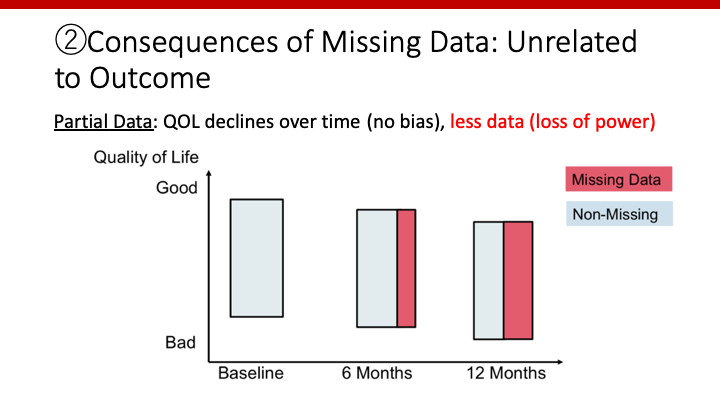
欠損値があり、欠損となるか否かがアウトカムと関連していない場合を考えてみます。赤色で示した範囲が、欠損値です。欠損はランダムに起きているため、存在するデータだけを解析しても、それぞれのタイミングで中央は変わりありません。6ヶ月後、12ヶ月後と、やはりQOLは低下していますね。従って、バイアスはありません。
ただし、経過とともにサンプルサイズが減っているため、その変化を統計学的に有意か調べる際の検出力(power)は低下しています。
③アウトカムと関係する欠損値がある場合
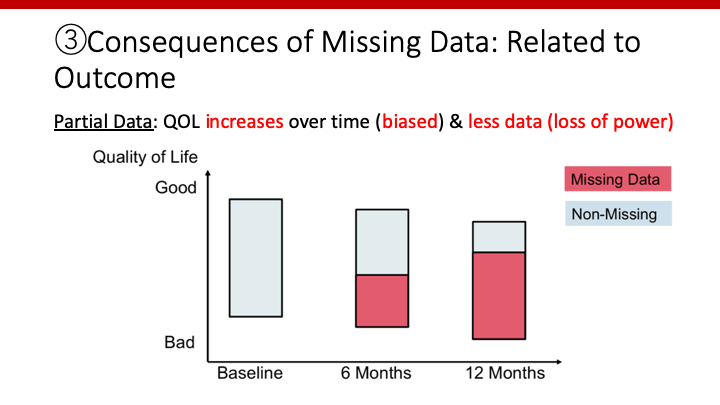
今度は、欠損値があり、かつそれがアウトカムと関連している場合です。時が経ち、QOLが低下した人ほど(病院に来れない、surveryに答えないなど)何らかの理由でQOLに関するデータが欠損しています。
すると、データがある人だけを調べた場合、それぞれの中央は半年後、1年後で(下がるどころか)上がっていますね。これがバイアスです。そしてもちろん、サンプルサイズが減っているので検出力も低下しています。
このように、一概に欠損値といっても、その性質によってデータの解釈を変えてしまう場合があることがわかります。
欠損値の種類
上記の例は、単に欠損値とアウトカムとの関係のみを考えました。しかし、欠損値の種類を考える場合には、ある因子の欠損値がその因子自体に関係しているかと、その他の因子に関係しているかを考えなければなりません。
Missing Completely At Random: MCAR

ある因子が欠損値となるかどうかが、その因子と関係なく、その他の因子とも関係ない場合です。この場合は、欠損値が完全にランダムとなることを意味しているため、変な解析をしない限りバイアスを引き起こすことはありません。一方で、実際のデータでこのような欠損値のパターンをとることは殆どありません。
上の例②は、QOLの欠損値がQOLを関連していないため、MCARか、次に説明するMARとなります。
Missing At Random: MAR

ある因子が欠損値となるかどうかが、その因子自体とは関係ありませんが、その他の因子とは関係がある場合です。
例えば、高齢であればある程収入に関するデータを報告しない(すなわち欠損)が、収入の高さは報告の有無に関係しない、といったケースです。
上の例②は、このMARとなり得ます。
現在使われているmissing dataに対する手法の殆どは、その欠損値がMCARまたはMARであるとの仮定に基づいています。
Missing Not At Random: MNAR

ある因子が欠損値となるかどうかが、その因子自体とも他の因子とも関係がある場合です。
例えば、収入が低ければ低いほど自分の収入を報告しない(収入の欠損値が収入と関連)、といったケースです。
最初の例③がこのMNARとなります。QOLという因子が欠損するか否かが、QOLによって変わってくるためです。
MNARであれば現在のメジャーな手法の殆どは、バイアスを取り除くことができません。
理論と実際

上記の欠損値の分類は、統計学的には非常に重要です。なぜなら、上記で述べたように、殆どの手法はMCAR(ほぼ非現実的)またはMARでのみ有効であるからです。
一方、実際はこれらの3種類を分類し証明することは不可能です。なぜなら、欠損値は欠損しているため、関連を調べることができないからです。
上記の分類は、あくまで理論的なものですが、それでも欠損値を扱う上では欠かせない概念です。
たとえrandomized controlled trialであっても、欠損値の種類によっては適切な手法を用いなければバイアスを生み出してしまいます。大きなgrantを勝ち取ろうとするのであれば、欠損値に対するアプローチについても、立案の段階でしっかりと明記する必要があります。
まとめ
欠損値は、その因子自体や他の因子との関連性によって、MCAR, MAR, MNARの三種類に分けられます。欠損値の種類によっては、適切な手法を用いなければ、バイアスを生み出し、検出力が低下します。
どのような手法があるのかは、今後解説していきたいと思います。
Reference
John Orav. EPI 522. Harvard T.H. Chan School of Public Health






コメント
コメント一覧 (2件)
[…] 欠損値(missing value)の種類:実際のデータ解析でほぼ必須となる欠損値の基本です。 […]
[…] サンプル数が小さい。41名中24名がpoor studyやpacemakerといった理由により除外されている。これらがmissing completely at random (MCAR)でない限り、除外はバイアスとなる。 […]