久々の疫学系の話題ですね。今回はメタ解析(meta-analysis)で用いる基本的な言語や概念について解説しようと思います。ちなみに、最後にはmeta-analysisで必要な”r”のコードも付記しています。
Effect measures(効果量の推定)
メタ解析の目的
メタ解析では、曝露・介入(exposure)による効果(effect)について調べた複数の研究を合わせ、その全体としての効果(combined effect)を評価することが目的です。その複数の研究の中でも、より正確な研究結果は重要視したいですよね。そのためには、単なる平均(mean)ではなく、それぞれの研究結果に重み付けを行なった平均(weighted mean)を計算します。
では、どのようにその重み付けを行い”combined effect”を計算するのでしょうか。メタ解析で用いられる重み付けの計算方法(モデルの作り方)には、固定効果モデル(fixed effect model)とランダム効果モデル(random effects model)が存在します。
Fixed effect(固定効果)
仮定
Fixed effect modelでは、全ての研究で効果の大きさ(effect size)は同じであると仮定します。すなわち、それぞれの研究の中で、個人個人に対する効果にはバラツキ(within-studies error)があっても、それぞれの研究の間での効果の大きさにバラツキ(between-studies error)がないと仮定しています。
数学的には、以下のように表せます。
Ti = μ + εi
※μ, true effect; Ti, observed effect in study i; εi, error within study i
重み付け
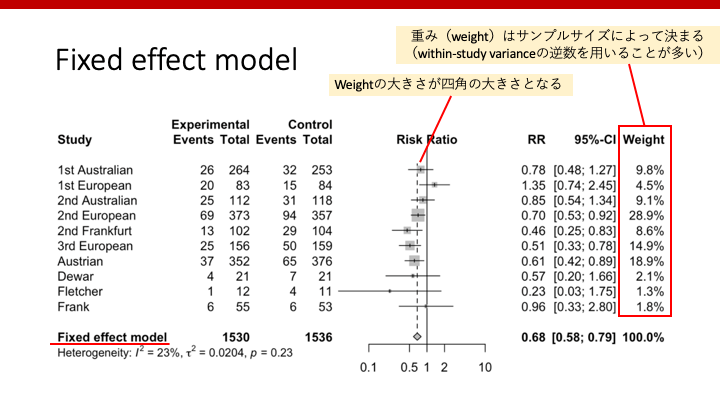
目的となる全体の効果の大きさ(combined effect)は、全ての研究間で同じであると仮定した効果量であり、それを推定するためには各研究に重み付けを行なった平均(weighted mean)を計算します。Fixed effect modelでは個々の研究の重みはそれぞれの研究の情報量に依存するため、サンプルサイズの大きな研究には大きな重みがかかり、小さな研究は無視されがちになります。
エラー
全体の効果の大きさのエラーは、個人個人のバラツキに由来(within-studies error)するため、大きなサンプルサイズであればそのエラーは小さくなります。これは、一つの研究が大きなサンプルサイズを持っていても、メタ解析に含んだ全ての研究の合計として大きなサンプルサイズとなったとしても、同じ結果になります。
通常、重み(weight)にはイベント数から計算したvarianceを用いますが、アウトカム(event)が発生しなかった群ではvarianceの計算ができません。そのような稀なeventがあるメタ解析では、Peto methodやMantel-Haenszel methodがfixed effect modelの重み付けとして使用されます。
Random effects(ランダム効果)
仮定
前述のように、fixed effect modelでは、全ての研究で効果の大きさは同じであると仮定しましたね。一方、Random effects modelでは、研究の間で効果の大きさにバラツキがあってもよいとします。例えば、ある研究では患者の年齢層が高い、より重症が多い、などといった理由により、ある曝露・介入(exposure)による効果(effect)が大きい(or 小さい)かもしれません。個人個人に対する効果にはバラツキ(within-studies error)に加え、そのような研究間での効果のバラツキ(between-studies error)も許容するのがrandom effect modelです。
数学的には、以下のように表せます。
Ti =θi + εi = μ + ei + εi
※μ, true effect; Ti, observed effect in study i; θi, true effect in study i; εi, error within study i; ei, between-study error for study i
重み付け
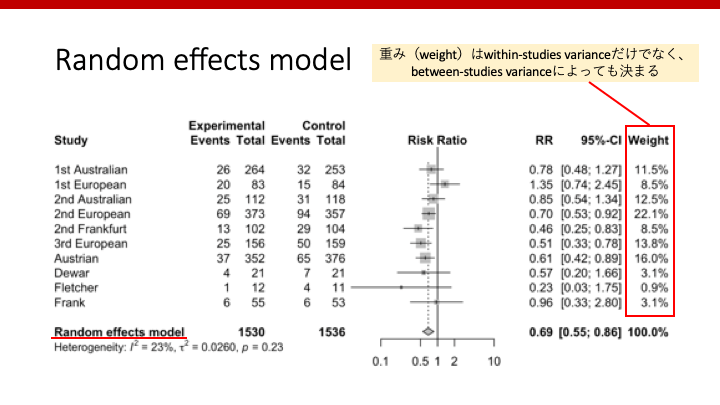
全体の効果の大きさを計算する際、fixed effect modelと同様、大きな研究には大きな重み付けが行われます。しかし、random effects modelではそれぞれの研究が異なる効果の大きさを持っても構わず、それらの平均が全体の効果(combined effect)になります。結果、fixed effect modelと比較し、バランスのとれた重み付けとなります。すなわち、大きな研究であっても重みは少し小さくなり、小さな研究であっても重みは少し大きくなります。Fixed effect modelと比べて研究間のバラツキも考慮できる利点はありますが、小さい研究を過大評価する危険性もあります。
エラー
Random effects modelでは、まず個々の研究における効果(effect)を推定した後、それらのeffectsから全体のeffectを計算しなければなりません。そのため、全体の効果の大きさのエラーは、個々の研究のサンプルサイズだけでなく、メタ解析に含まれる研究の数にも由来することになります。研究数が少ないと、それぞれの研究のeffectの分布から全体のeffectを推定(平均)することが難しく、推測値が不正確になります。
細かい話になりますが、random effects modelでは効果量(effect size)のbetween-studies errorは考慮していますが、varianceのerrorまでは考慮していません。解決方法としては、Hartung-Kanapp MethodやProfile likelihood、Bayesian random effectsなどが提唱されています。
Heterogeneity(異質性)の評価
Q statistic
研究間での異質性(Heterogeneity)を評価するためには、between-studiesのバラツキ(→variance)を評価する必要があります。
Total variance = within-studies variance + between-studies variance
という関係性から、between-studies varianceを推定します。以下のような手順でbetween-studies varianceを評価します。
- 全てのvarianceの”指標”である、Q statisticを計算する。
- 全ての研究で同じ効果量を持つものと仮定した場合に予想されるvarianceの”指標”である、df(=number studies – 1)を求める。
- (Q – df)はvarianceの超過分となり、これ(を変形したもの)がbetween-studies varianceを表し、tau-squared(τ2)と呼ばれる。
また、①Q statisticを②dfによるχ2分布とすることでp-valueを計算し、統計学的にheterogeneityを検定することもできます。帰無仮説は「全ての効果量(θi)は等しい」ですので、p-value <0.05であれば棄却し、「heterogeneityあり」となります。
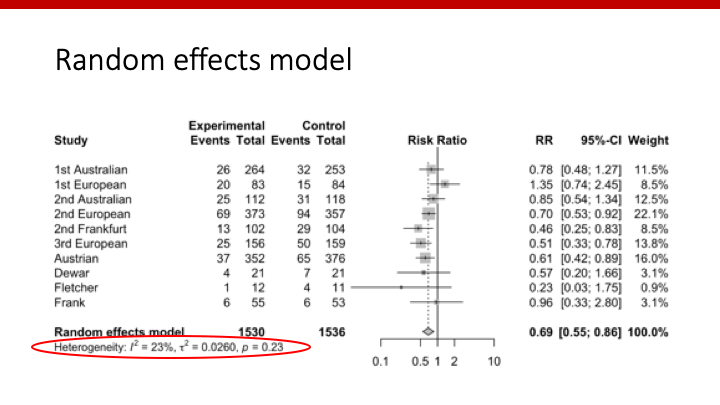
ちなみに、Q statisticは全てのvarianceを反映しますが、その計算式(ここでは省略)をみればわかるように、個々の研究のvarianceの逆数で重み付けされています。すなわち、Q statisticは、total varianceの”指標”ではありますが、そのものではなく、total varianceとwithin-studies varianceの比に依存しています。
一方で、Q statisticは厳密にはχ2分布ではない、研究数が少ないと検出力が低い、といった欠点も指摘されています。
I2 statistic
上のスライドにも載っていますが、Q statistic以外にもI2という指標もあります。
I2= (Q – df)/Q * 100 (≒ τ2/(τ2 + s) * 100)
という計算により0から100の数値でheterogeneityを表現します。一般的には、
- 0% – 40%: might not be important
- 30% – 60%: may represent moderate heterogeneity
- 50% – 90%: may represent substantial heterogeneity
- 75% – 100%: considerable heterogeneity
と言われています。
もしheterogeneity (異質性)を認めた場合には、サブグループ解析やmeta-regressionを用いることで、なぜ研究間でなぜ効果に差があるのか、どのような条件下で効果があるのか、といったことを調べることができます。
Publication bias(出版バイアス)
Funnel Plot
臨床研究では、サンプルサイズの大きな研究では統計学的に有意な結果であろうがなかろうが出版(publish)される傾向にありますが、サンプルサイズの小さな研究では大きな効果量(effect size)の時のみ出版される傾向にあります。また、有意な結果が出た臨床研究のみが出版されるかもしれません。
このようなバイアスを見つけるための一つの方法がfunnel plotです。Funnel plotでは、x軸に効果量、y軸に1/standard errorをとり、それぞれの研究をplotしていきます。サンプルサイズの大きな研究は効果の大きさの推定値がより正確になると考えられますので、一般的には大きな研究は平均近くに位置し、小さな研究は平均から離れ、分布は左右対称になります。しかし、有意な結果が出た臨床研究のみが出版された場合など、そのような対称な分布になりません。
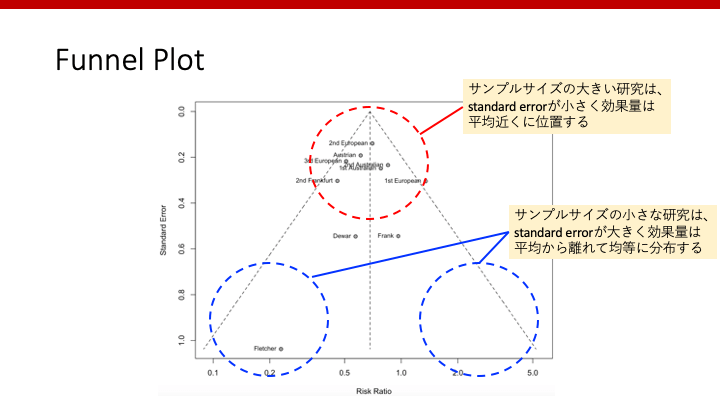
Egger’s test
x軸を”1/standard error”、y軸を”effect estimate/standard error”とした、回帰分析(regression model)を用いても、出版バイアスを評価することができます。
数式で表すと、以下のようになります。回帰分析に関しては、こちらをご覧ください。
θ/se = b0 + b1 * 1 / se
この回帰直線の切片(b0: intercept)が「バイアス」となり、上記のfunnel plotにおける「非対称性」を表す数値になります。小さなサンプルサイズの研究で大きな効果量(effect estimate)を示す場合に、この切片は大きくなり、出版バイアスの存在が示唆されます。
ただし、検出力は高くありません。特にmeta解析に含まれる研究数が10未満の場合には、使用しないほうが無難でしょう。
参考
いかがでしたでしょうか。メタ解析を行う側、読む側になったときに、少しでも参考になれば幸いです。ちなみに、上記で用いたrのコードを以下に載せておきます。
library(meta)
# Fixed effect model
meta_se<-metabin(deaths1,pop1,deaths0,pop0,data=df_2,studlab=paste(trialnam),comb.fixed=T,comb.random=F,sm="RR")
forest(meta_se)
# Random effects model
meta_se_r<-metabin(deaths1,pop1,deaths0,pop0,data=df_2,studlab=paste(trialnam),comb.fixed=F,comb.random=T,hakn=T,sm="RR",method.tau = "EB")
forest(meta_se_r)
# Funnel plot
funnel(meta_se,studlab=T)
# Egger's test
eggers.test<-function(data){
data<-data
eggers<-metabias(data)
intercept<-as.numeric(eggers$estimate )
intercept<-round(intercept,digits=3)
se.intercept<-eggers$estimate
)
intercept<-round(intercept,digits=3)
se.intercept<-eggers$estimate lower.intercept<-as.numeric(intercept-1.96*se.intercept)
lower.intercept<-round(lower.intercept,digits = 2)
higher.intercept<-as.numeric(intercept+1.96*se.intercept)
higher.intercept<-round(higher.intercept,digits = 2)
ci.intercept<-paste(lower.intercept,"-",higher.intercept)
ci.intercept<-gsub(" ", "", ci.intercept, fixed = TRUE)
intercept.pval<-as.numeric(eggers$p.value)
intercept.pval<-round(intercept.pval,digits=5)
eggers.output<-data.frame(intercept,ci.intercept, intercept.pval)
names(eggers.output)<-c("intercept","95%CI","p-value")
title<-"Results of Egger's test of the intercept"
print(title)
print(eggers.output)
}
eggers.test(data=meta_se)
lower.intercept<-as.numeric(intercept-1.96*se.intercept)
lower.intercept<-round(lower.intercept,digits = 2)
higher.intercept<-as.numeric(intercept+1.96*se.intercept)
higher.intercept<-round(higher.intercept,digits = 2)
ci.intercept<-paste(lower.intercept,"-",higher.intercept)
ci.intercept<-gsub(" ", "", ci.intercept, fixed = TRUE)
intercept.pval<-as.numeric(eggers$p.value)
intercept.pval<-round(intercept.pval,digits=5)
eggers.output<-data.frame(intercept,ci.intercept, intercept.pval)
names(eggers.output)<-c("intercept","95%CI","p-value")
title<-"Results of Egger's test of the intercept"
print(title)
print(eggers.output)
}
eggers.test(data=meta_se)
References
- Stefania I. Papatheodorou. EPI 233: Systematic Review and Meta-analysis. Harvard T.H. Chan School of Public Health
- Schober P et al. Anseht Analog 2020. PMID 32925329.

 )
intercept<-round(intercept,digits=3)
se.intercept<-eggers$estimate
)
intercept<-round(intercept,digits=3)
se.intercept<-eggers$estimate lower.intercept<-as.numeric(intercept-1.96*se.intercept)
lower.intercept<-round(lower.intercept,digits = 2)
higher.intercept<-as.numeric(intercept+1.96*se.intercept)
higher.intercept<-round(higher.intercept,digits = 2)
ci.intercept<-paste(lower.intercept,"-",higher.intercept)
ci.intercept<-gsub(" ", "", ci.intercept, fixed = TRUE)
intercept.pval<-as.numeric(eggers$p.value)
intercept.pval<-round(intercept.pval,digits=5)
eggers.output<-data.frame(intercept,ci.intercept, intercept.pval)
names(eggers.output)<-c("intercept","95%CI","p-value")
title<-"Results of Egger's test of the intercept"
print(title)
print(eggers.output)
}
eggers.test(data=meta_se)
lower.intercept<-as.numeric(intercept-1.96*se.intercept)
lower.intercept<-round(lower.intercept,digits = 2)
higher.intercept<-as.numeric(intercept+1.96*se.intercept)
higher.intercept<-round(higher.intercept,digits = 2)
ci.intercept<-paste(lower.intercept,"-",higher.intercept)
ci.intercept<-gsub(" ", "", ci.intercept, fixed = TRUE)
intercept.pval<-as.numeric(eggers$p.value)
intercept.pval<-round(intercept.pval,digits=5)
eggers.output<-data.frame(intercept,ci.intercept, intercept.pval)
names(eggers.output)<-c("intercept","95%CI","p-value")
title<-"Results of Egger's test of the intercept"
print(title)
print(eggers.output)
}
eggers.test(data=meta_se)




コメント
コメント一覧 (1件)
[…] メタ解析の基本と必須用語:メタ解析の論文に必要な、fixed effect, random effects, heterogeneity, publication biasなどについての解説です。 […]