あるアウトカムを予測するためには回帰モデル(regression model)を使う方法が(特に医療界では)有名ですが、方法はそれだけではありません。サンプルをあるルールに沿って木の枝のように次々と分けていく、決定木(decision tree)という予測モデルの作り方も、機械学習領域ではとても有名です。
今回は、この決定木(decision tree)の基本的な概念について、Pythonのコードを使用しながら解説したいと思います。
ちなみに、専門用語を英単語のまま記載、または併記している部分があります。これは、個人的に「決定木」などと無理やり日本語に訳すことに違和感があるからです。申し訳ありませんが、悪しからず。
目的
一応、準備段階のコードを載せておきますが、decision treeの概念を理解するだけなら飛ばしていただいて構いません。
# ライブラリ
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# モデル作成のため
from sklearn import ensemble, impute, metrics, preprocessing, tree
from sklearn.model_selection import cross_val_score, train_test_split
from sklearn.pipeline import Pipeline
# その他のカスタム
from IPython.display import display, HTML, Image
plt.rcParams.update({'font.size': 20})
%matplotlib inline
plt.style.use('ggplot')
import datathon2 as dtn
import pydotplus
from tableone import TableOne
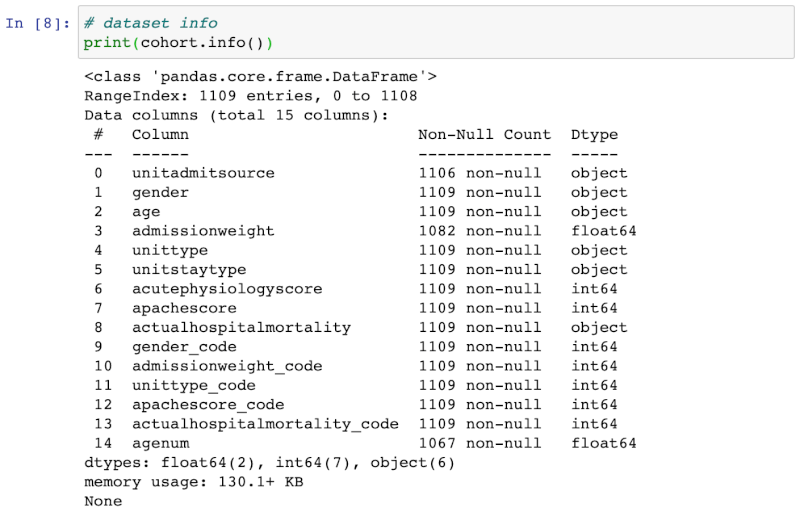
このデータセットから、
年齢(age)と重症度スコア(acutephysiologyscore_code)の二つに注目してモデルを作成することにします。すなわち、
ICU初日の「年齢」と「重症度スコア」という二つの予測因子によって、「院内死亡」というアウトカムを予測する
ことが目的です。
トレーニングセットとテストセットを作成
まず、抽出したデータを、トレーニングセット(モデルを作るためのデータセット)とテストセット(モデルのパフォーマンスを測るためのデータセット)に分けます。
features = ['age','acutephysiologyscore'] outcome = 'actualhospitalmortality_code' X = cohort[features] y = cohort[outcome] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=10)
予測モデルを作る際、そのモデル作成の元データで幾ら良いモデルであっても、他のデータに対して用いてパフォーマンスが悪ければ意味がありません。そのため、「トレーニングセット」でモデルを作り、「テストセット」で実際のパフォーマンスを比較します。
Decision trees
Classification tree
今回はアウトカムが生存・死亡という2つのカテゴリー(binary outcome)を持つので、それぞれの患者をそれぞれのカテゴリーへ出来るだけ正確に分類(classification)することが目的となります。
Treeによるモデルの作成をClassification and Regression Trees (CART)と総称します。今回はアウトカムがカテゴリーなので”classification tree”を用いますが、連続変数をアウトカムとする”regression tree”も平均値を用いた同じような方法になります。
クラス分けを主とするclassification treeでは、あるルールを元にデータを次々と木の枝のように分け(split)、最終的な葉っぱの部分の中にあるサンプルをその多数が属するクラスへ割り当てます。
Splitが一回のみ
まずは、最もシンプルな、splitが一回のみのdecision treeを考えてみましょう。一回のみsplitした場合(stump)、データは二群に分けられ、それぞれの群は多数が属するクラスへと割り当てられます。この割り当てられたクラスが、モデルの予測となります。
# Splitを一回のみに指定したtreeを作成 mdl = tree.DecisionTreeClassifier(max_depth=1) # どのようなtreeになったかを説明するため、同じトレーニングセットでアウトカムを予測 mdl = mdl.fit(X_train,y_train)
出来上がったdecision treeを図示すると、以下のようになります。
graph = dtn.create_graph(mdl,feature_names=features) Image(graph.create_png())
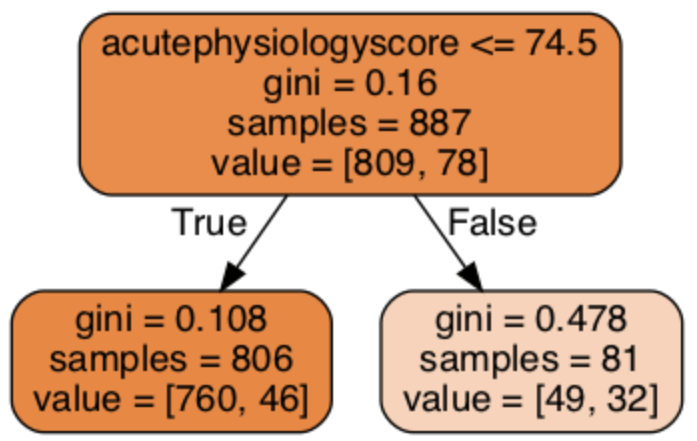
三つのnode(四角に囲まれた部分)に注目していきます。まずは、全てのデータを含んだ一番上にあるnodeを見ていきましょう。
value = [809, 78]: クラス分け前のアウトカムです。809人の生存(class = 0)と、78人の死亡(class =1)が確認できます。samples = 887: サンプル数の合計です。gini = 0.16: “Gini”は、”impurity (不純・混入)”の指標です。Gini impurityが低いということは、クラス分けが成功していることを意味します。クラスが半々(クラス分けが不成功)の場合、Giniは0.5となります。acutephysiologyscore <=74.5: このnodeに適応されるsplitのルールです。今回は重症度スコアが74.5以下であれば左のnodeへ分けられることになります。
このdecision treeではGiniを指標にsplitのアルゴリズムが決定されます。すなわち、split後の二つのGini impurityが最も低くなるように、モデルの予測因子(年齢 or 重症度スコア)とそのカットオフポイントが選ばれます。このようなsplitの選択方法を”greedy”と呼びます。
Impurityを測る方法として、”Gini Index”と”Entropy”の2つが有名です。Pをそのアウトカムとなるprobabilityとすると、以下のように計算されます。
- Gini Index = 2P(1-P)
- Entropy = -Plog(P) – (1-P)log(1-P)
また、impurity以外にも統計学的なテストや分類後の感度・特異度を元にsplitを決定する方法もあります。
どのようにクラス分けされたのか、x軸に年齢を、y軸に重症度スコアを配置した二次元の図で見てみましょう。
plt.figure(figsize=[10,8])
dtn.plot_model_pred_2d(mdl, X_train, y_train,
title="Decision tree (depth 1)")
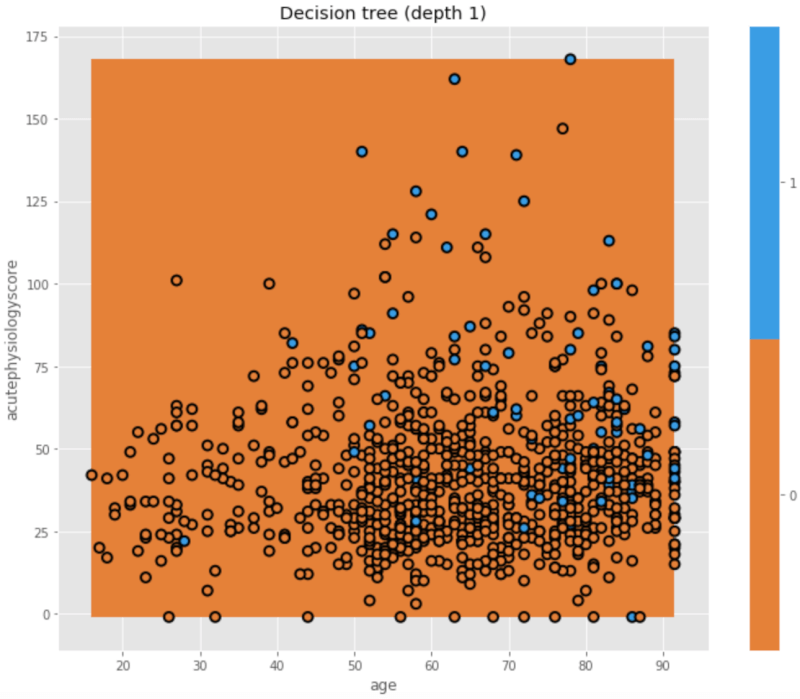
それぞれの点の色が本当のクラス(生存 or 死亡)を表しており、背景の色がその予測になっています。背景の色と点の色が異なる場合、クラス分けの不一致(misclassification)を示します。今回は、重症度スコア(y軸)=74.5で分けたtreeでしたが、分けた後のどちらのnodeも生存の方が多かったため、結局どちらも「生存」と予測された(背景は全てオレンジ色)、ということを示しています。
Splitを増やす
Splitを増やすことでtreeのdepthを増やし、複雑なモデルにしてみましょう。
mdl = tree.DecisionTreeClassifier(max_depth=5)
mdl = mdl.fit(X_train,y_train)
plt.figure(figsize=[10,8])
dtn.plot_model_pred_2d(mdl, X_train, y_train,
title="Decision tree (depth 5)")
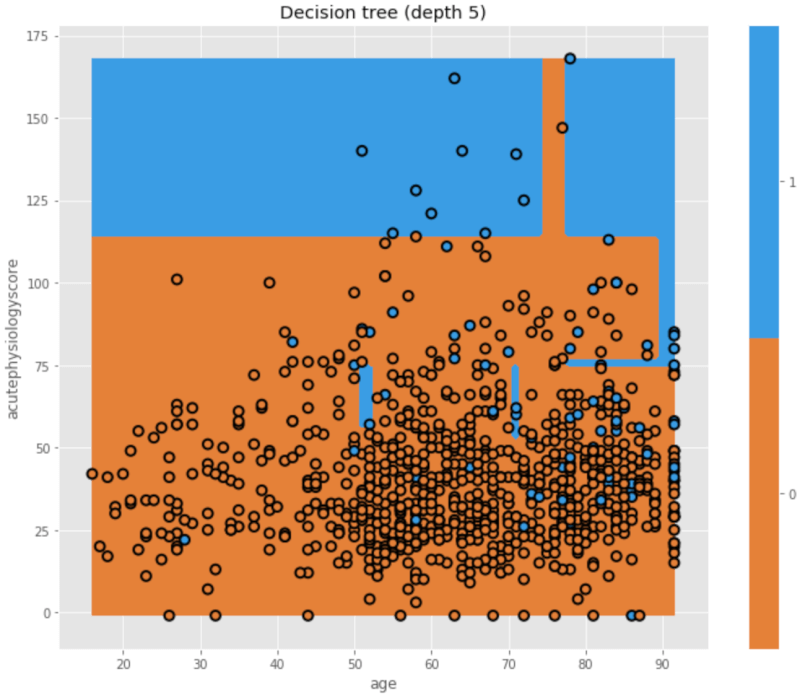
いかがでしょう。このモデルでは、x軸・y軸ともに複数回splitに使われて、背景の色分けが複雑になっているのがわかりますね。どのようなsplitになったか、tree自体を見てみましょう。
graph = dtn.create_graph(mdl,feature_names=features) Image(graph.create_png())
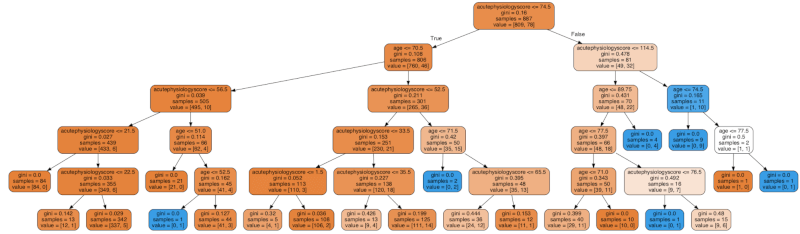
重症度スコアが50、年齢が71歳の患者を例に考えてみます。
- acutePhysiologyScore <= 74.5? Yes.
- age <= 70.5? No.
- acutePhysiologyScore <= 52.5? Yes.
- age <= 71.5. Yes.
と、この患者は「gini impurity = 0(100%生存 or 100%死亡)」のnodeに行き着きます。臨床現場を考えるとこのように完璧なクラス分けは不可能に思われますが、このアルゴリズムでGiniのみを根拠にsplitするとこのようになります。これが、いわゆる”overfit“(←「多変量解析の変数は何個まで入れて良いのか」でも説明していますので、よろしければ参照してください)です。
Pruning
Decision treeでは、前述のoverfitを回避するため、“pruning(枝を切り取る)”を行います。
# 先ほど作成したtree (mdl)を"prune"していきます mdl = dtn.prune(mdl, min_samples_leaf = 20) graph = dtn.create_graph(mdl,feature_names=features) Image(graph.create_png())
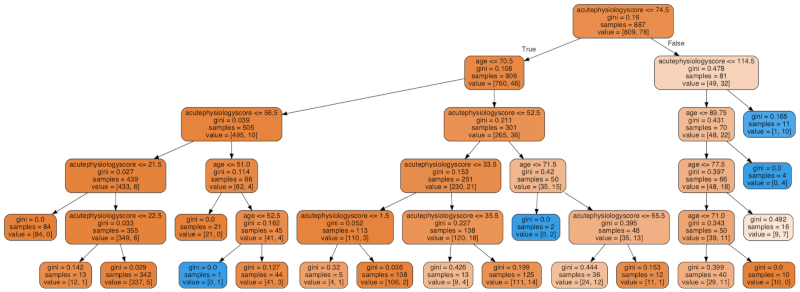
min_samples_leaf=20と設定することにより、20サンプル以下のnodeはそれ以上splitされないようになっています。二次元図では、
plt.figure(figsize=[10,8]) dtn.plot_model_pred_2d(mdl, X_train, y_train, title="Pruned decision tree")
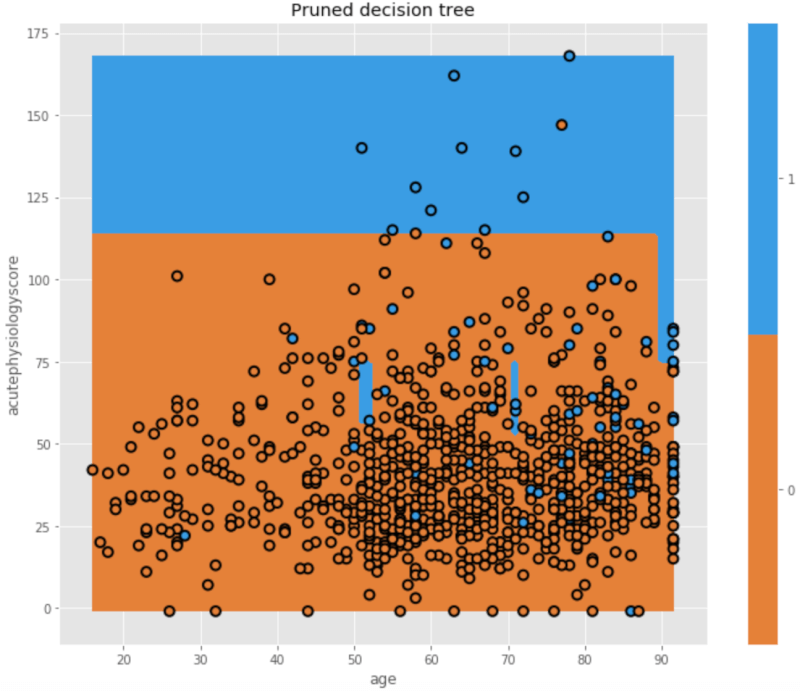
のようになっています。このようにpruningされたtreeは、臨床家としては直感的に理解しやすい、比較的シンプルなモデルになることが多いですが、その代わりに予測のエラーは増えてしまいます。これが機械学習でよく言われる、モデルの複雑性とエラーのトレードオフです。
Decision treeとvariance
Desicion treeでは、variance(分散)が大きくなる傾向にあります。すなわち、モデルの元となるトレーニングセットのサンプルによって、毎回そのモデルが大きく変わってきます。以下に、データをランダムに抜き取り、モデルを複数作ってこのvarianceについて説明します。
fig = plt.figure(figsize=[12,3])
# 試しにtreeを3つ作成
for i in range(3):
ax = fig.add_subplot(1,3,i+1)
# データを抽出するためのランダムな数字を作成
idx = np.random.permutation(X_train.shape[0])
# 最初の50サンプルのみを使用
idx = idx[:50]
X_temp = X_train.iloc[idx]
y_temp = y_train.values[idx]
# モデルの作成
mdl = tree.DecisionTreeClassifier(max_depth=5)
# 予測
mdl = mdl.fit(X_temp, y_temp)
txt = 'Random sample {}'.format(i)
dtn.plot_model_pred_2d(mdl, X_temp, y_temp, title=txt)
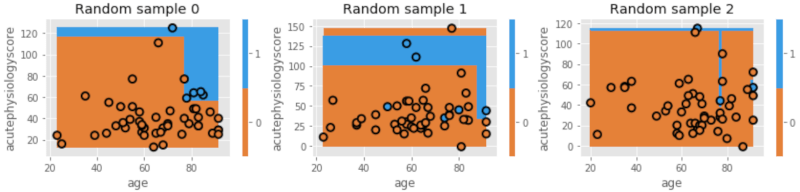
このように、データをランダムに抽出しモデルを作成した際、それぞれのモデルの境界線は毎回大きく異なっています。
しかし、このように大きなvariance(分散)を持つdecision treeを組み合わせることで、小さなvarianceを持つ一つのモデルを作り上げることが可能になります。すなわち、幾つもモデルを組み合わせることで、良いモデルができあがります。これが、BoostrapやRandom Forestといった複数のTreeを組み合わせる考え方の元になります。
まとめ
今回は、Decision treeの基本的な概念と、最もシンプルなtreeの作成方法について解説しました。次回は、このdecision treeを複数組み合わせて、Boosting (AdaBoost), Bagging, Random Forest, Gradient Boostingといったより良いモデルを作り出す方法について解説しようと思います。
参考文献
- Tom Pollard. HST 953. Prediction and Classification Tree. Massachusetts Institute of Technology.
- Nancy Cook and Fran Cook. EPI 288. Data Mining. Harvard T.H. Chan School of Public Health
- Gareth James et al. “An Introduction to Statistical Learning” with Application s in R.






コメント
コメント一覧 (1件)
[…] 前回は、決定木(decision tree)の基本的な概念について説明しました。前回の最後のところで触れたように、decision treeは複数組み合わせることによってより良いモデルになる可能性があります。そこで今回は、Boosting (AdaBoost), Bagging, Random Forest, Gradient Boostingといった、複数のtreeを組み合わせて一つのモデルを作り上げる方法について解説したいと思います。 […]