連続変数の表すための基本用語

今日は、連続変数の分布を表すために必要な「言語」について説明したいと思います。

ちなみに、今回の多くはハーバード公衆衛生大学院のJohn Oravの講義を元に自分なりにまとめたものです。目からウロコの毎日だったので、興味があれば受講してみてはいかがでしょうか。夏だけの短期講習（Program in Clinical Effectiveness）であればdegreeのような受験勉強も不要です。

連続変数のsummary statistics

今回は、この1~4についてです。それぞれが何を意味しているのでしょう。

分布のcenter

「センター」といっても、その表し方は一つではありません。

(a)は平均です。それぞれの数を合計し、サンプル数で割ると出ますね。例えば、datというdata frameのBMIというcolumnの平均を出したければ、

> # Average of BMI
> sum(dat$BMI)/nrow(dat)
 25.84616
> mean(dat$BMI)
 25.84616
> summary(dat$BMI)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  15.54   23.09   25.45   25.85   28.09   56.80

のような方法でみることができます。

(b)は中央値です。平均は外れ値によってひっぱられるので、中央値の方がデータによっては優れた表現であることがあります。上のsummary()でも中央値を得ることができます。

分布の広がり

(a) 広がりを表す言葉として、variance（分散）があります。それぞれのデータの平均値からのズレを2乗し合計することで、データがどのくらいvariabeなのかわかります。

(b)Centerの議論と同様、IQR (interquartile range)という考え方があります。データを小さい順に並べ、前1/4番目と前3/4番目の数字です。100人いた場合、medianが50番目であるのに対し、25th percentileは25番目の数字ということになります。こちらもsummary()で求めることができます。

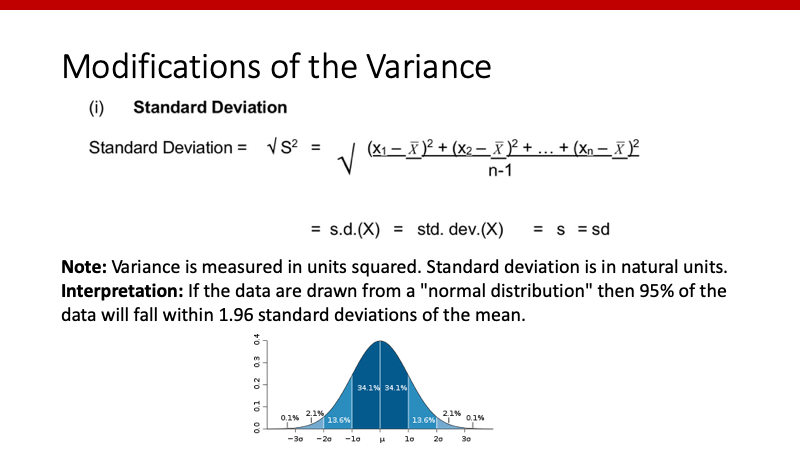
Standard deviation（標準偏差）は、varianceをルートしたものです。これにより、varianceと異なりデータの広がりを元データと同じ単位で表すことができます。ちなみに、正規分布である場合は1.96*SDに95%のデータが含まれることになります。

Standard error（標準誤差）は、varianceをサンプル数で割った数のルートです。解釈としては、平均値のvarianceと考えます。リピート実験を行なった際、その平均値はどの程度ばらつくのか、です。今回は一回のみの実験ですが、上記のようなSDとの関係によりSEを求めることができます。すなわち、

Standard error = 平均値のstandard deviation

ということができます。

> # Variance
> var(dat$BMI)
 16.82493
> # Standard deviation
> sqrt(var(dat$BMI))
 4.101821
> sd(dat$BMI)
 4.101821
> # Standard error
> sd(dat$BMI)/sqrt(length(dat$BMI)) 
 0.06173214

サンプル数が多くなれば平均値は安定しSEは小さくなる一方で、SDはより安定するだけです。サンプル数が大きいからといって皆が平均に近づいたりしませんね。

データが個々でどのくらい異なるのか、その広がりを示したいならSDを書きます。論文のresultsの最初の部分で、患者データの全体の分布を述べるときなどに使います。

一方で、平均値を比較（他で説明しますが、t-testやregressionなど多くはmeanを比較している）する場合は、SEを使います。SDもSEも、論文では”±”で表記するため、その違いを理解する必要があります。

分布の対称性

対称性を示す言葉として、skewness（歪度）があります。以下のように、正規分布であればskewnessは0となり、meanとmedianは一致しますが、非対称であればskewnessは０から離れます。（完璧な）正規分布の一条件としてskewness=0があるんですね。

外れ値の多さ

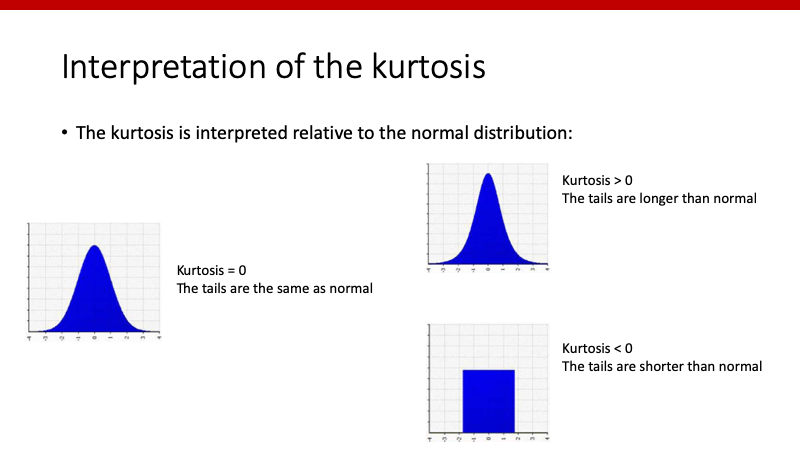
尖度とも訳されるkurtosis。分布のbodyとtailのバランスを表します。ソフトフェアによっては自動的に3を引いてoutputするものもあります。その場合、kurosis=0が正規分布の一条件になります。

ちなみに、skewnessもkurtosisを含め、psychというパッケージを使えば以上で述べてきた値を一発で簡単に求めることができます。

>library(psych)
>describe(dat$BMI)
   vars    n  mean  sd median trimmed  mad   min  max range skew
X1    1 4415 25.85 4.1  25.45   25.57 3.68 15.54 56.8 41.26 0.98
   kurtosis   se
X1      2.6 0.06

今回は、連続変数を評価する上で必要な共通言語を説明しました。

 

⇒医療従事者に必要な統計学と疫学（目次）へ

 

References

John Orav. BST 206: Introductory Statistics for Medical Research. Harvard T.H. Chan School of Public Health