交絡（confounding）と交互作用（effect modification)

臨床研究データを解析する際、混乱しやすい用語の中に、交絡（confounding）と交互作用（effect modification )があります。統計学的にはどちらも層化（stratification）により判断することがあり、両者を混同してしまうことが多いようです。とても重要な概念ですので、両者の違いをしっかりと理解しておきましょう。

はじめに

まず初めに、confoundingとeffect modificationがどのようなものなのか、簡単な例を挙げて考えてみましょう。

交絡（confounding）

Confoundingとは、ある因子（ex. Yellow fingers）とoutcome（ex. Lung cancer）の両者に影響を与えるものです。下の例ですと、肺癌がその二つの関係をconfoundしているケースです。

まずは、単純にyellow fingersとlung cancerの関係を見てみましょう。

Risk ratioが3.06ですので、yellow fingersのない人に比べ、yellow fingersがある人は肺癌に3倍以上なりやすいことになります。では、yellow fingersは肺癌の原因なのでしょうか。喫煙の有無によって層化（stratirication）してみましょう。

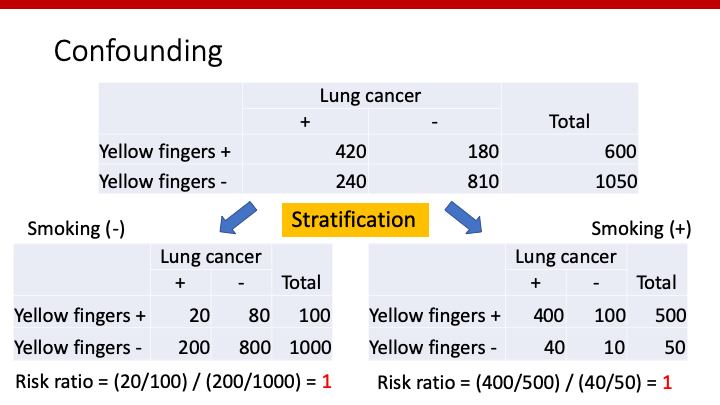
このように、喫煙の有無でstratificationした場合、どちらもrisk ratioは1となり、yellow fingersと肺癌には関連がないことがわかります。すなわち、肺癌を引き起こしているのは喫煙であり、指が黄色いから肺癌になる訳ではない、ということです。喫煙で層化した前後で、yellow fingersと肺癌の関係性が変化したため、喫煙は（統計学的には）confounderと言えます。

交互作用（effect modification )

Effect modificationとは、ある暴露（ex. β遮断薬）とoutcome（死亡）の関係性を変化させる因子がある場合のことを言います。Effect modificationもまた、stratificationによって明らかにすることができます。

以下の例は、周術期のβ遮断薬の使用が死亡率に与える影響を調べたものです。

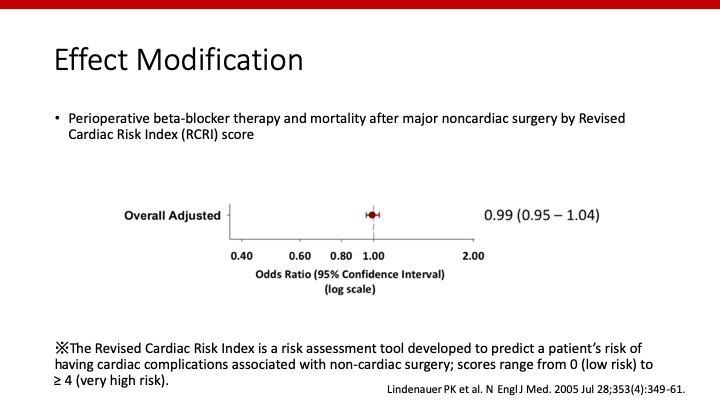
単純な解析ですと、そのodds ratioは0.99 [0.95-1.04]となり、β遮断薬は死亡率に影響を与えていないと判断されます。

では、RCRIという患者の重症度スコアによってstratificationしてみましょう。

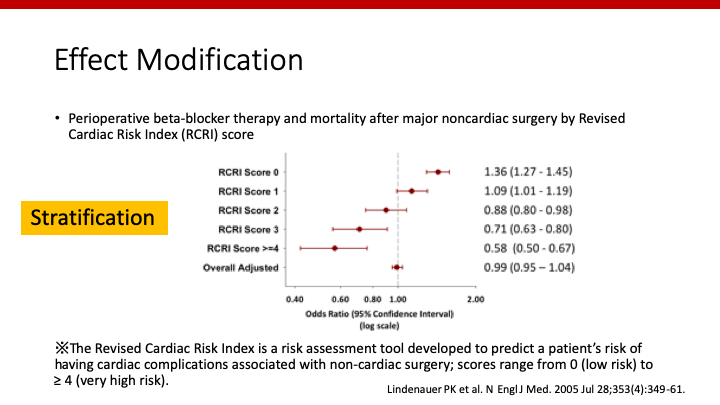
面白いですね。重症な患者ではβ遮断薬によって死亡率が低く（ex. Score>=4: Odds ratio 0.58 [0.50-0.67]）、軽症な患者ではβ遮断薬によって死亡率が髙い（ex. Score=0: Odds ratio 1.36 [1.27-1.45]）ことがわかります。すなわち、β遮断薬は死亡に影響を及ぼさないと一概に言うことは間違っており、ある患者には効くし、ある患者には逆効果である、ということです。RCRIによってβ遮断薬の死亡に対する”effect”が”modification”されている、ということですね。

Confounding vs. Effect modification

ある二者の関係性を変化させる第三の因子

Confoundingもeffect modificationも、ある二つの関係性を変化させる第三の因子という点では同じです。しかし、confoundingの場合はある因子を一定にした場合の前後でその二つの関係性が変化するのに対し、effect modificationはある因子別に分けた場合にそ因子別で関係性が異なる場合に使います。

よりわかりやすくするため、図にしてみましょう。左図ではsmokingがconfounder、右図ではsmokingがeffect modifierとなっています。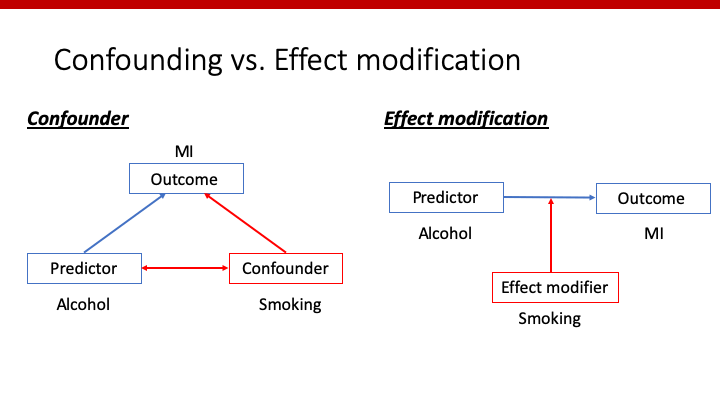

Confounding

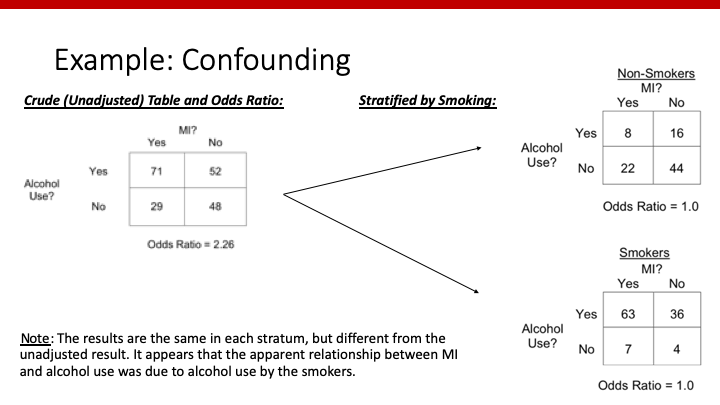
喫煙でstratificationする前のodds ratioが2.26であったのに対し、stratification後のodds ratioが1.0と変化しています。「前後」で異なるのがconfoundingです。

Effect modification

一方、effect modificationであった場合には、喫煙でstratificationした後の階層別（喫煙あり群と喫煙なし群）のodds ratioが1.0と5.67と異なっていることがわかります。「階層別に異なる」ものが、effect modificationです。

実際の手順

では、stratificationでどのようにconfoundingやeffect modificationを見つけ出すのか、実際の手順をご紹介します。

Step 0

まずはともあれ、stratificationを行う前の二者の関係性を評価してみましょう。今回は、喫煙（CURSMOKE=1）が死亡（DEATH=1）に与える影響（crude odds ratio）を調べたいとします。

# Making 2 by 2 table
tab<-xtabs(~CURSMOKE+DEATH,data=dat)
tab

##         DEATH
## CURSMOKE    0    1
##        0 1486  755
##        1 1392  782

# Easy way to get OR and confidence interval
library(DescTools)
OddsRatio(tab,method="wald",conf.level=0.95)

## odds ratio     lwr.ci     upr.ci 
##  1.1057053  0.9768793  1.2515201

となり、喫煙者の死亡に対するoddsは、非喫煙者のそれよりも1.10倍高い[95% CI 0.98-1.25]ということがわかります。

Step 1

次に、stratificationを行いましょう。今回は、性別（malesex）によって層化します。そして、それぞれの階層において、知りたい二者の関係性を計算します。

# 2 by 2 table stratified by sex
tab <-xtabs(~ CURSMOKE+DEATH + malesex, data=dat)
tab

## , , malesex = 0
## 
##         DEATH
## CURSMOKE    0    1
##        0 1050  423
##        1  728  275
## 
## , , malesex = 1
## 
##         DEATH
## CURSMOKE    0    1
##        0  436  332
##        1  664  507

# For female
OR_female<-OddsRatio(tab[,,1],method="wald",conf.level=0.95)
OR_female

## odds ratio     lwr.ci     upr.ci 
##  0.9376705  0.7841131  1.1212999

# For male
OR_male<-OddsRatio(tab[,,2],method="wald",conf.level=0.95)
OR_male

## odds ratio     lwr.ci     upr.ci 
##  1.0027399  0.8344704  1.2049405

Stratificationした結果、女性における（死亡に対するoddsを非喫煙者と喫煙者で比較した）ORは0.94、男性におけるORは1.00でした。

補足ですが、ggplot2を使えば綺麗な図によって視覚的に捉えることができます。

library(ggplot2)
est_s<-as.data.frame(rbind(OR_female,OR_male))
est_s<-add_rownames(est_s,"label")
#est_s$label<-factor(est_s$label,c("OR among female","OR among male"))
ggplot(data=est_s, aes(x=label, y=`odds ratio`, ymin=lwr.ci, ymax=upr.ci)) +
  geom_pointrange() + 
  geom_hline(yintercept=1, lty=2) +  # add a dotted line at x=1 after flip
  scale_x_discrete(label = c("Female","Male"))+
  coord_flip() +  # flip coordinates (puts labels on y axis)
  xlab("Stratification") + ylab("Odds Ratio (95% CI)") +
  theme_bw()+
  theme(axis.text.x = element_text(size=15), axis.title=element_text(size=15,face="bold"), axis.text.y = element_text(size=15))

 

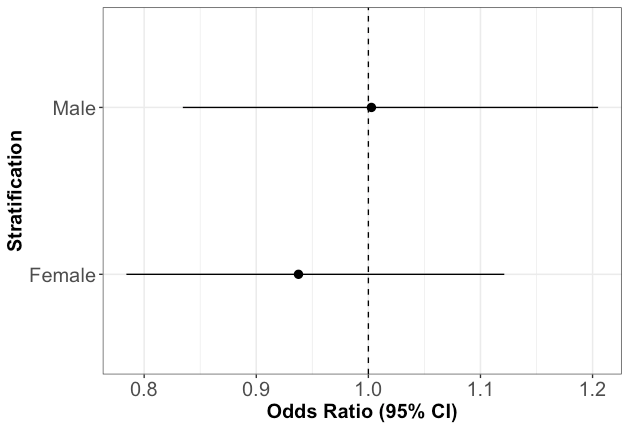
Step 2

階層別の二者の関係性が、それぞれ異なっているか否かを判断します。統計学なので、できれば検定で判断したいですよね。そこで用いるのが、Breslow-Day testです。帰無仮説は「階層別の関係性が同じ」です。

BreslowDayTest(tab ,OR=NA, correct=FALSE)

##  Breslow-Day test on Homogeneity of Odds Ratios
## 
## data:  tab
## X-squared = 0.26309, df = 1, p-value = 0.608

p=0.61ですので、帰無仮説を棄却できません。すなわち階層別の関係性が異なるとは言えない、ということです。

Breslow-Day testの注意すべき点は、Shapiro-Wilk testと同じです。サンプルサイズが小さければORが大きく違っても帰無仮説を棄却できず「同じ」と言ってしまう可能性があり、サンプルサイズが大きすぎるとoverpowerとなり、ORがほぼ同じであっても「違う」と言ってしまうことがあります。

Step 2a

階層別のORが異なっていないと判断した場合、effect modificationは無いと判断します。Effect modificationが無い場合は、層別にORを提示する必要がありません。その場合、次のステップは層別のORを一つにまとめる（adjusted odds ratio）ことが可能になります。Mantel-Haenszel testでadjusted ORを求めることができます。

mantelhaen.test(tab, correct=F)

##  Mantel-Haenszel chi-squared test without continuity correction
## 
## data:  tab
## Mantel-Haenszel X-squared = 0.23583, df = 1, p-value = 0.6272
## alternative hypothesis: true common odds ratio is not equal to 1
## 95 percent confidence interval:
##  0.8522924 1.1011105
## sample estimates:
## common odds ratio 
##         0.9687456

そして、このstratification後のadjusted ORがstratification前のcrude ORと（10%または20%以上）異なる場合、confoundingありと判断します。今回のadjusted OR=0.97ですので、crude OR =1.10と比較し12%減少しています。10%をcut-offにした場合は、性別はconfounderということになります。

Step 2b

階層別のORが異なっていると判断した場合、effect modification有りと判断します。その場合、層別にORを提示してください。Crude ORを提示しては駄目ですし、まとめてadjusted ORを提示してもいけません。そして、stratification後のadjusted ORを計算してはいけないため、stratification前後でORを比較することができません。すなわち、（統計学的には）confoundingの有無を検討することができません。

まとめ

Stratificationを行なうことによってconfoundingとeffect modificationをどのように比較しているのかを図示しています。

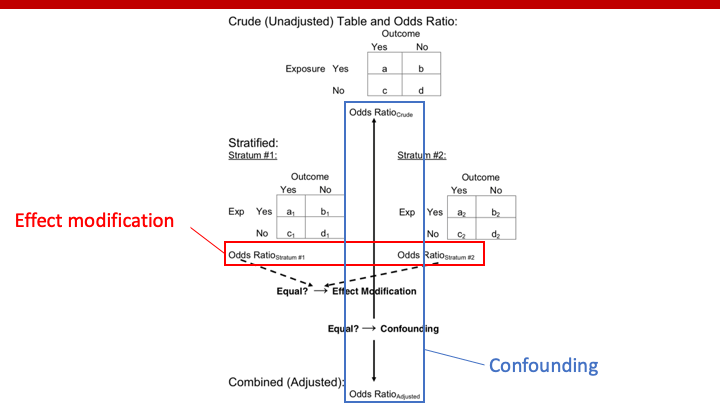
いかがでしたか？ややこしい二者ですが、その違いは理解できましたでしょうか。

 

⇒医療従事者に必要な統計学と疫学（目次）へ

References

• John Orav. BST 206: Introductory Statistics for Medical Research. Harvard T.H. Chan School of Public Health
• John Orav. BST 208: Stats for Med Research, Advanced. Introductory Statistics for Medical Research. Harvard T.H. Chan School of Public Health
• Murray A. Mittleman. EPI 201: Introduction to Epidemiology: Method 1. Harvard T.H. Chan School of Public Health
• Murray A. Mittleman. EPI 202: Epidemiologic Method 2: Elements of Epidemiologic Research. Harvard T.H. Chan School of Public Health
• John Orav. BST 213: Applied Regression for Clinical Research. Harvard T.H. Chan School of Public Health