正規分布の評価方法

先に申し上げておきますが、その判断は結構主観的です。統計といったら数字で全て説明できそうですが、意外に個々の主観が入ってきます。大事なのは、正規分布か否かを判断したその手順をしっかり説明できることだと思います。

1) ヒストグラム

Rのggplot2というパッケージは、data visualizationにおける最高のツールの一つです。もしRを使うなら、是非とも使えるようになりたいパッケージです。ggplot()+geom_histogram()を使うことでヒストグラムを描くことができます。datというdata frameのBMIというcolumn（連続変数）のヒストグラムを描いてみましょう。

library(ggplot2)
dat%>% ggplot()+
  geom_histogram(aes(BMI),binwidth =1)

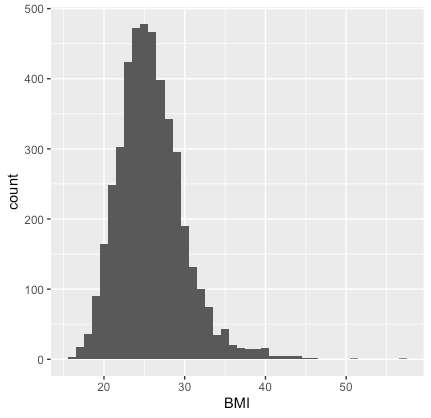
これがbell-shapeかどうかです。どうですか？Bell-shapeにみえますか？

2) Skewnessとkurtosis

2)は、連続変数の評価：skewnessやkurtosistとは？で説明しました。

> describe(dat$BMI)
   vars    n  mean  sd median trimmed  mad   min  max range skew kurtosis   se
X1    1 4415 25.85 4.1  25.45   25.57 3.68 15.54 56.8 41.26 0.98      2.6 0.06

ちなみに、このサンプル群においてskewnessは0.98、kurtosisは2.6です。

3) QQ plot と 4) Shapiro-Wilk test

次に、QQ plotというグラフを描きます。実際のn個のデータを小さい順から並べ、同じ平均値とstandard deviationを持つ正規分布からランダムに得られたn個の値を計算します。元のデータが正規分布であれば、それぞれのペアをplotすると直線となります。こちらも同じパッケージのggplot()+stat_qq()で描くことができます。

dat%>%ggplot(aes(sample=BMI)) + stat_qq()

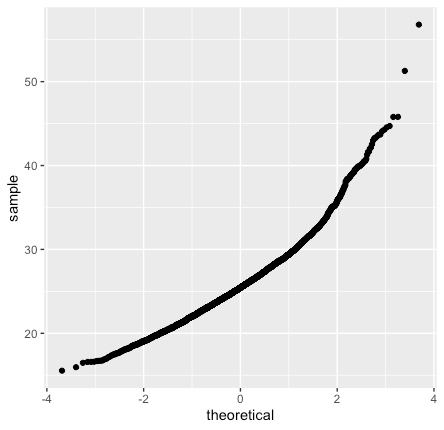
そして最後にnormalityの検定であるShapiro-Wilk testを行います。nが多い時などは他の検定方法も使いますが、今回はShapiro-Wilk testを使ってみようと思います。

> shapiro.test(dat$BMI)
	Shapiro-Wilk normality test
data:  dat$BMI
W = 0.95734, p-value < 2.2e-16

p<.001であるため、「正規分布である」という帰無仮説を棄却することになります。

しかし、その結果を鵜呑みにしてはいけません。サンプルサイズが大きければ、この検定はoverpowerになってしまい、完璧なnormality以外は棄却してしまいます。逆に、サンプルサイズが小さければunderpowerとなり、明らかにnormalでなくても棄却できません。

いかがでしょうか。ある人はこう言います。

しかし、ある人はこう言います。

これ、どちらも正解なんです。正規分布かどうか、どのように考えたか説明できて筋が通っていればokなんです。

HSPHのJohn Oravの凄いところは、統計学者でありながら、医療従事者がどのようなデータを扱い、どのように解釈するかを理解しているところです。統計学者は数字を元に答えを求めたがりますが、医師は臨床現場における解釈が重要です。彼の口癖は「It depends」でした。

⇒医療従事者に必要な統計学と疫学（目次）へ

Reference