MENU
医師が留学の体験談・失敗談をシェアするブログ
  1. ホーム
  2. 医療統計と疫学
  3. カテゴリー vs. カテゴリー: Z-test, Chi-square, and Fisher

カテゴリー vs. カテゴリー: Z-test, Chi-square, and Fisher

医療統計と疫学

今回は、カテゴリー変数とカテゴリー変数の関連を調べる方法について解説したいと思います。

例えば、男女で急性腎不全（AKI）の発生率に違いがあるのか、といった命題です。男女は「男性=1, 女性=0」の変数となり、AKIは「AKI発生あり=1, AKIなし=0」の変数となります。

目次

Binomial Distribution

統計学的には、それぞれの人が、ある一定の確率pでAKIが発生すると考えます。AKIとなれば1、AKIでなければ0です。n数の患者がpの発生率で0 or 1となることを、Binomial (n, p) distributionと呼びます。

ある患者XiがAKIとなる確率は、

P(Xi=1)

で表され、これがpですね。

もちろん、それぞれの患者はAKIになるか、ならないか、なので、X自体は0 or 1ですが、その期待値E(Xi)はpとなります。

n人の患者において、i人がAKIとなる確率は、

P(Y=i)

で表され、これがnCipi(1-p)n-iとなります。

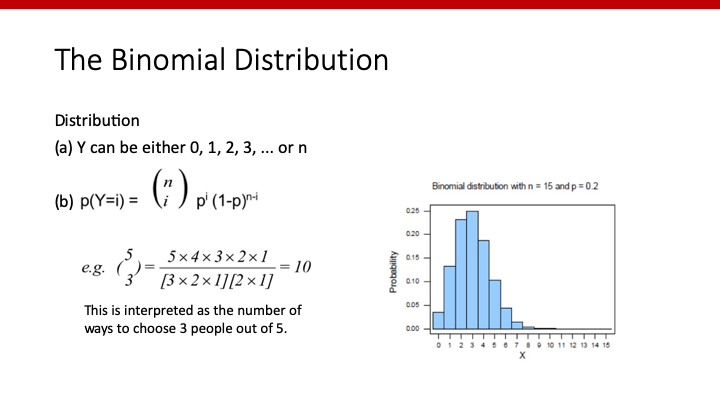
上のスライドの右図は、n=15、p=0.2のときのprobabilityのグラフです。15 * 0.2=3なので、15人いたら3人AKIとなる可能性が最も高いですが、もちろん2人かもしれませんし、4人かもしれません。それらのprobabilityを描いたもの、それがbinomial disributionです。

2群のbinomial distributionの比較

ここでは例として「心筋梗塞（MI）の既往がある患者は、MIの既往のない患者と比較し、MIとなる頻度が異なるのか？」を比較したいとします。

すなわち、MIの既往のある群（X群）におけるMIとなるprobability (px)と、MIの既往のない群（Y群）におけるMIとなるprobability（py）を比較する、ということです。

まず、2×2の表（two-by-two table）を作りましょう。

Null hypothesisは、両群のMIとなるprobabilityが同じ（px=py）です。

このHoを検定するために、大きく分けて3つの方法があります。

1. Approximate Approach – Comparison of two proportions (Risk Difference) by a Z-Test

2. Approximate Approach – Chi-square Test

3. Exact Approach – Fisher’s Exact Test 

 

一つ一つ見ていきましょう。

1. Comparison of Two Proportions: z-test

連続変数におけるmeanの比較では、その差とvarianceさえわかればz-testを使えるんでしたね。

「Null hypothesis：両群のMIとなるprobabilityが同じ（px=py）」を検定するためにも、pxとpyの差とvarianceがわかればz-testが使えることになります。

このように、px, py, varianceが計算できるので、z-scoreとconfidence intervalも以下のように計算できます。

後述するように、z-testから得られたp-valueはchi-squareから得られたp-valueと同じです。また、z-testは、power calculationの時に必要となります。

2. Chi-Square Test

帰無仮説

z-testでは、両群のprobabilityが同じかどうかを考えました。Chi-squareでは、同じ意味で違う問いかけを考えます。今回の例でしたら、

MIの既往とMIになるかどうかは独立しているか

です。

Null hypothesisも、

MIの既往のある場合のMIとなるprobability[P(MI|History)]と、MIの既往のない場合のMIとなるprobability[P(MI|No-History)]が同じである

となります。

P(A)とP(B)が独立している場合、P(A∩B) = P(A) * P(B)なので、上のスライドのような式が成り立ちます。

H0下におけるexpected numbers

p-valueとは、帰無仮説が成り立っている条件下での今回のようなtest statisticまたはそれよりextremeな値をとるprobabilityのことでした。今回のような「independent」という帰無仮説の元、それぞれのcellに入るべき数字（expected number)が計算できます。

スライド右下の青四角で囲ってある部分に、例として2-by-2 tableにおける左上のcell（MIあり、Historyあり）に入るexpected numberの計算式を示しています。Independentであるという帰無仮説があるので、「P(A∩B) = P(A) * P(B)」を使うことができ、計算することが可能となります。

Chi-squareのdistribution

z-testではz-distributionにおけるz-scoreのprobabilityを、ANOVAではF-distributionにおけるprobabilityを計算したのと同様、Chi-square testでもχ2のdistributionにおけるχ2のprobability (=p-value)を計算します。

χ2は、それぞれのcellにおける今回の値からH0下でのexpected numberを引いた値を2乗し、そのexpected numberで割った値を、全部のcellで足し合わせた数と定義されます。

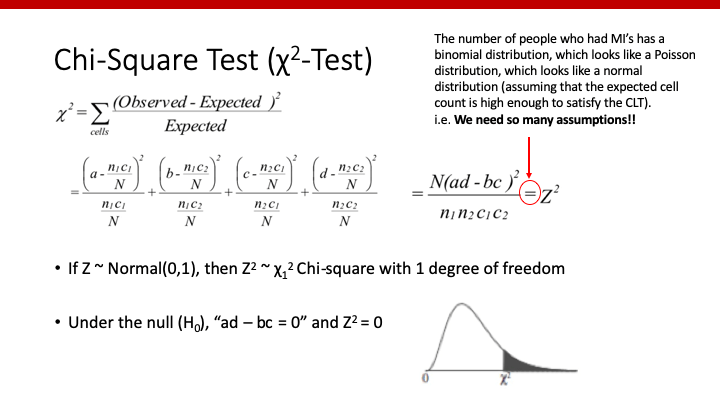
このχ2、様々なassumption（後述）の元、実はz-scoreの2乗と等しくなります。したがって、χ2の分布を考える際、z-distributionを2乗したものと考えることができます。normal (0,1)であるz-distributionを2乗することで、上のようなχ2のdistributionができあがります。

あとは、そのχ2distributionにおける、今回のχ2がのprobabilityを求め、それがp-valueとなります。

帰無仮説が正しい場合、χ2は0となりますが、これは分子のad-bc=0を意味しますね。ad=bc i.e. ad/bc=1となりますので、Odds Ratio (OR)=1となります。

よく論文で、ORの横にp-valueが書かれていますが、その根拠はここにあります。Chi-square testの帰無仮説はOR=1と同じであるため、ORのp-valueにChi-square testのp-valueを載せても良いことになります。

今回の例ですと、以下のようにχ2は11.47になります。

下図は、χ2とprobabilityの関係を図示したものです。

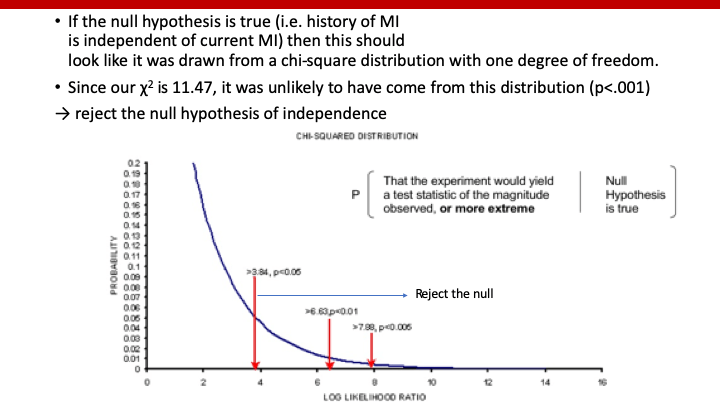
χ2>=11.47取りうるprobabilityは、0.001未満でしたので、p<0.0001となります。

ちなみに、p=0.05となるcut-offは、z=1.96と同じなので、χ2=z2=1.962=3.84となります。

χ2がz2となるには、様々なassumptionが必要になります。詳細は述べませんが、

Binomial distribution→Poisson distribution→normal distribution (using Central Limit Theorem)

と変化させる必要があります。ですので、サンプルサイズが小さい場合などではこのassumptionが崩れるため、chi-squareで求めたp-valueは間違っている可能性が高くなります。

Rを使ってみましょう。

# One way
chisq.test(dat$malesex,dat$STROKE,correct=F)

# Another way (using table and package)
library(DescTools)
tab<-xtabs(~malesex+STROKE,data=dat)
chisq.test(tab,correct=F)

Chi-squareの注意点

・Chi-squareは常に両側p-valueです。なぜなら、z-scoreを2乗したものなので、2乗した後はone-sidedでも元はtwo-sidedだからです。

・Chi-square testのdegree of freedomは1です。なぜなら、cellのどれかが決まれば（n1, n2, c1, c2がわかっているため）他のcellも決まるからです。

・今回はtwo-by-two tableを考えましたが、chi-squareはもっと大きいtable (ex. four-by-four table）にも使えます。その場合、もし有意差があったとしても、どのcombinationに有意差があるのかはわかりません。

z-test vs. chi-square test

前述のように、chi-squareのdistributionはzの2乗のdistributionであるため、chi-square testとz-testは同じp-valueとなります。

z-testはpower calculationに用いられるという点で有用なのに対し、chi-square testは2-by-2よりも大きなtableでも用いられることが有用です。

z-testは2群のprobabilityの差を検定しているので、2-by-2だけに対して使えます。

3. Fisher’s Exact Test

Chi-square testでは、χ2というスコアが、その分布においてとりうるprobabilityを考えることによって、p-valueを導き出していました。ある分布であると仮定した上で導き出したp-valueですので、これは厳密には正確なp-valueではありません。そういった意味で、Z-testもChi-square testも、approximate approachということができます。

一方、p-valueの定義は、帰無仮説が成り立っている条件下での今回のようなtest statisticまたはそれよりextremeな値をとるprobabilityでした。Category vs. categoryの表では、このprobabilityを直接計算することができます。

これは、MIの既往の有無とMIの発生には関係がない（独立している）といった条件下での、今回のようなデータまたはそれよりもextremeな値をとりうるprobabilityを計算したものです。

例えば、最初のP()は、500人中47人がMIである場合の中で、「MIの既往のある122中21人がMIとなった」かつ「MIの既往のない378中26人がMIとなった」確率（今回のような研究結果となるprobability）を計算したものです。P-valueとは、それよりもextremeとなるprobabilityも考えなければなりませんので、全てのケースを足し合わせています。

このように得られたp-valueは、p-valueの定義そのものであるため、正確なp-valueということができます。そのため、Fisher’s exact testと呼ぶんですね。

もちろん、Rを使って検定できます。上記と同様、2つの方法を書いておきます。

# One way
fisher.test(dat$malesex,dat$STROKE)
# Another way
fisher.test(tab)

 

Chi-square vs. Fisher’s exact test

最後に、Chi-square testとFisher exact testの違いを要約して書いておきます。

Chi-square test

  • p-valueが正確な値ではなく、大体の値である。
  • 手計算でも求められる。
  • 表の1つのcellに5以上のサンプルがある場合に特に有効。
  • サンプルサイズが小さいとp-valueが不正確。

Fisher’s exact test

  • p-valueが正確。
  • 手計算では求めるのは大変。
  • ソフトフェア（パソコン）を用いても時間がかかるし、サンプル数によっては計算が困難。

このような特徴があるため、可能であればFisher’s exact testを用い、サンプルサイズが大きくなればChi-square test、といった感じで使っていけば良いのではないでしょうか。

 

以上です。カテゴリー変数同士を比較する場合、何が何でもChi-square testを使えば良いのではないんですね。

 

⇒医療従事者に必要な統計学と疫学（目次）へ

 

Reference

  • John Orav. BST 206: Introductory Statistics for Medical Research. Harvard T.H. Chan School of Public Health
医療統計と疫学
よかったらシェアしてね！
  • URLをコピーしました！
  • URLをコピーしました！

関連記事

コメント

コメント一覧 （1件）

コメントする

英語のコメントは『問い合わせ』からお願いします。

目次