t-testとWilcoxon rank sum test

ここでは、2群間で連続変数を比較する検定方法について解説します。一般的に有名なのはt-testとWilcoxon rank sum testですが、どのように両者を使い分けるのでしょうか。

はじめに

大まかには、上記のスライドのように考えていきます。2群とも正規分布であれば、上記の「Yes」となり、Z-testかt-testが選べます。ただ、後述するようにZ-testは非現実的なので、現実的にはt-testを選ぶことになると思います。

2群のどちらかが正規分布でない場合、「No」に進みます。サンプルサイズが大きければ、中心極限定理（Central Limit Theorem: CLT）を用いてt-testを使うことが可能になります。もちろん、正規分布というassumptionを置かないWilcoxon rank sum testを使うことも可能です。

正規分布でなくサンプルサイズが小さければCLTが使えないため、Wilcoxon rank sum testの一択になります。

では、それぞれの検定法について解説していきましょう。

Z-test

比較する両群のvarianceがわかっているなら、Z-testを用いることができます。上記のようにZ-scoreを計算し、Z-distributionにおけるそのscoreまたはそれ以上の値を取りうるprobabilityを計算することで、p-valueを得ることができます。今の一文の意味がわからない人は、正規分布とprobabilityを読んでみてください。

しかし、我々は母集団のvarianceを知ることができません。知ることができるのは、我々の研究対象となった両群のvarianceのみです。そのため、使うべきはZ-testではなくt-testとなります。

t-test

t-testを使う場合でも、両群のvarianceが等しい場合と異なる場合でt-scoreもt-distributionも若干異なります。等しい場合は左式を、異なる場合は右式を用います。t-scoreからprobabilityを計算する過程も、ココをご覧ください。

Varianceが等しい場合には

t.test(dat$BMI[dat$malesex==1],dat$BMI[dat$malesex==0],
var.equal = T)

Varianceが異なる場合には

t.test(dat$BMI[dat$malesex==1],dat$BMI[dat$malesex==0],
var.equal = F)

として検定します。

Varianceの検定

では、2群のvarianceが等しいかどうか、どのように判断するのでしょうか。ここでは、F-testを用います。

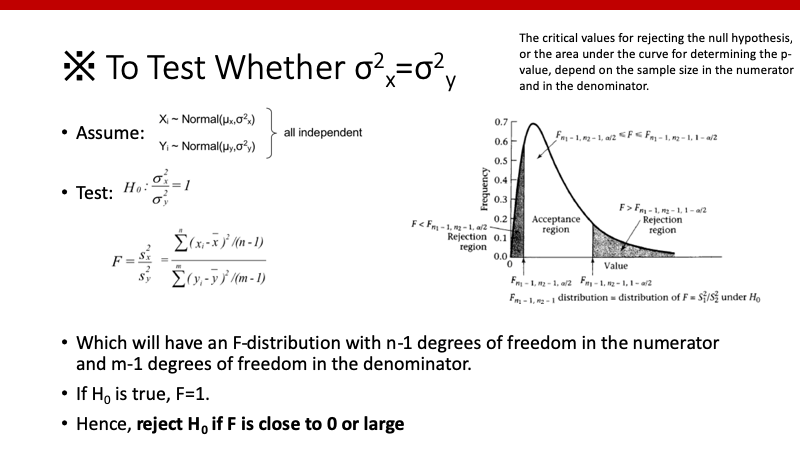
両群のvarianceが等しければ、F-scoreは1となり、異なれば1より離れます。どの程度離れればそのprobabilityが0.05よりも小さくなるかのcutoffは、degree of freedomに依存します。Rでは、以下のcodeを用いてください。

# Test whether s2x=s2y
var.test(dat$BMI[dat$malesex==1],dat$BMI[dat$malesex==0])

Wilcoxon Rank Sum Test

データが正規分布しておらず、サンプルサイズが小さい場合はCLTを使えません。その場合は、Wilcoxon rank sum testを用います。t-testの場合と異なり、連続変数そのものの値は用いません。全体を並べて小さい順にランキングをつけ、そのランクの平均値を比べます。

ランクさえつけてしまえば、Z-test（またはt-test）と同じです。用いるdistributioによってp-valueは若干ことなります。t-distributionの方がtailが大きいため、そのp-valueは大きくなります。

Rを用いると、

wilcox.test(dat$BMI[dat$malesex==1],dat$BMI[dat$malesex==0],correct = F,conf.int = T)

 

Powerという観点から

t-testとWilcoxon rank sum testの両方が使える場合、どちらを選択すべきでしょうか。Power（検出力）という観点からは以下のような感じになります。

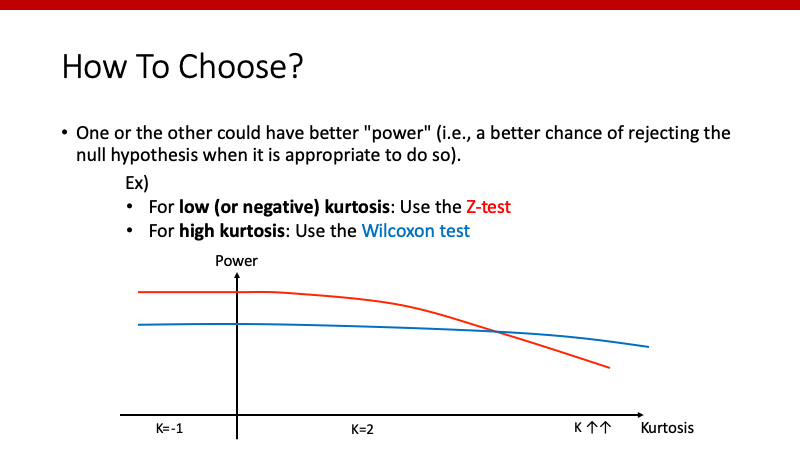
正規分布の場合は、t-testの方が強いpowerを持ちます。Wilcoxonを使うことによるpowerの低下は、サンプルサイズが約5%低下するのと同じくらいだそうです。

正規分布から離れると、場合によってはWilcoxonの方が強いpowerとなります。

以上です。いかがでしたでしょうか。t-testとWilcoxon rank sum test、理解が深まったでしょうか。

 

⇒医療従事者に必要な統計学と疫学（目次）へ

Reference

John Orav. BST 206: Introductory Statistics for Medical Research. Harvard T.H. Chan School of Public Health