今回は、3群以上で連続変数を比較する検定法について勉強します。まずはANOVAからやりましょう。
ANOVA
ANOVAを使うためには、幾つか満たすべきassumptionがあります。
Assumption

ここでは、わかりやすく3群で比較する場合を考えていきます。分散分析が使うためには、
1. それぞれの群での連続変数が正規分布であること
2. データが独立していること
3. 3群それぞれの分散が等しいこと
がassumptionとして必要になります。
1の正規分布の評価に関しては、こちらを参考にしてください。
2は意外に重要です。ICU入室患者を対象とした研究において、複数回入室した患者がいるとします。その場合、それらのデータはindependentではなくなってしまいます。例えば、n=10しかないのに、1人がICUに100回入室していた場合を考えてみましょう。データの数を9+100=109としてしまっては、データ全体がその一個人の傾向に引っ張られてしまいますよね(データがdependent)。その場合、「ICUの初回入室」といったfilterをかけることで、independentを保つことができます。
3が成り立ってない場合、データをtransformする方法や、weighted regressionという特殊な回帰分析を行う方法もありますが、c)のように無視してANOVAを使うことが現実的には多いように思います。
以上のassumptionがあった上で、ANOVAという分散分析が使えます。
F-scoreとは
他の検定と同様、分散分析においても帰無仮説の条件下で何らかのスコアを計算し、そのスコアをとりうるprobabilityを計算することによってp-valueを得ることができます。ANOVAの場合、帰無仮説は「3群の全ての平均は等しい」であり、その条件下で以下のようにF scoreを計算します。

分子は、それぞれの群の平均値から全体の平均値を引いたものの2乗を合計したものになりますので、各群の平均値がどのくらい全体の平均値から離れているかの指標になります。すなわち、3群の平均値が同じならF-scoreは小さく、バラバラになればなるほどF-scoreは大きくなります。
このF-scoreですが、もう一つの解釈方法があります。

このように、分子は群間の分散、分母は群内の分散という風に解釈することもできます。
理論的にはF-scoreは0をとりうるはずですが、実際のデータでは約1がほぼ最小らしいです。なので、どの群であっても違いがない場合はF-scoreは約1、群間に大きな差があったらF-scoreが大きくなり、H0をrejectする、という流れになります。
このF-scoreがF-distributionにおいてどのくらいrareなのか、その確率がp-valueです。F-scoreとF-distributionに関しては、t-testで2群の分散が等しいか否かの検定に用いたF-testを参照してください。
ちなみに、これら分散の関係を図示すると、以下のようになります。
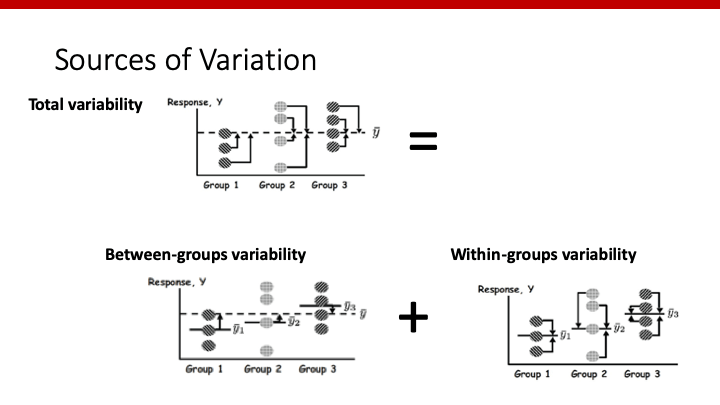
分散の合計 = 群間の分散 + 群内の分散
です。
ANOVAによる実際のoutput

これは、SASのoutputです。51404というのがvariability between groupsであり、1960というのがvariability within groupsとなります。従って、
F-score = 51404 / 1960 = 26.2
となり、今回のF-distributionにおけるprobability (p)が0.0001未満だったということを意味しています。
Rで解析してみましょう。dat_1というdata frameにおいてrace間でbwtを比較してみます。
ANOVAのコードは、
anova<-aov(bwt~race, data=dat_2)
summary(anova)Outputとしては、
## Df Sum Sq Mean Sq F value Pr(>F)
## race 2 5076973 2538487 4.978 0.00783 **
## Residuals 186 94850291 509948
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1となり、SASと同様のoutputを得ることができます。
図示するのであれば、
summarySE(dat_2,measurevar = "bwt", groupvars = "race")%>%
ggplot(aes(x=race, y=bwt, colour=race)) +
geom_errorbar(aes(ymin=bwt-se, ymax=bwt+se), width=.1) +
geom_point()+
scale_x_discrete(labels=c("White","Black","Others"))とすることで、
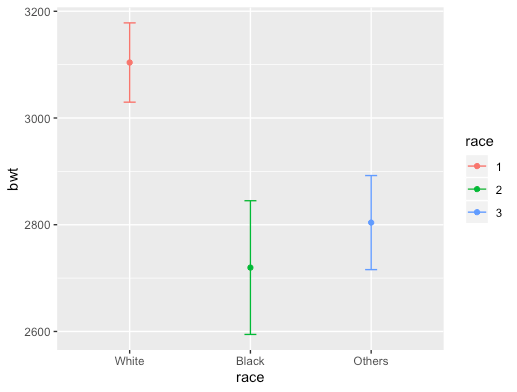
のような図を書くことができます。
Kruskal-Wallis Test
2群比較の時のように、それぞれの群のデータが正規分布しておらず、サンプルサイズが小さくcentral limit theoremが使えない場合は、ANOVAを用いることができません。その時には、non-parametricであるKruskal-Wallis testを使います。

詳細は割愛しますが、理論的にはWilcoxonと同じです。連続変数にランキングをつけ、データそのものではなく、そのランキングの平均値を群間で比べるということですね。
Rのcodeは
kruskal.test(dat_2$bwt ~ dat_2$race)##
## Kruskal-Wallis rank sum test
##
## data: dat_2$bwt by dat_2$race
## Kruskal-Wallis chi-squared = 8.5909, df = 2, p-value = 0.01363を使います。
Wilcoxonの時と同様、rankingを比較するのであればmeanの図を使うのはオススメできません。せめてbox plotで妥協しましょう。
dat_2%>%ggplot()+
geom_boxplot(aes(race,bwt),outlier.shape=NA)+
scale_x_discrete(labels=c("White","Black","Others"))+
xlab(label="Race")+
ylab(label="Birth weight")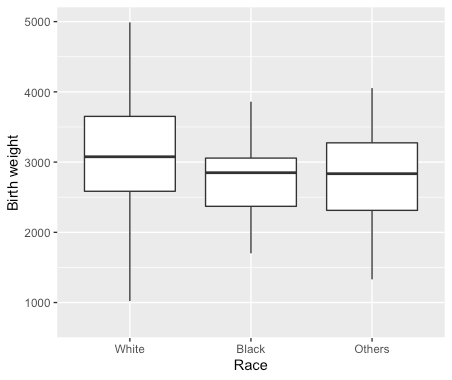
次は、群間で有意差があった場合のpairwise comparisonについてやりたいと思います。






コメント
コメント一覧 (6件)
[…] ANOVAやKruskal-Wallisで有意差がでたら、次はどのペアに有意差があるのかを調べるためのpairwise comparisonsを行います。 […]
[…] z-testではz-distributionにおけるz-scoreのprobabilityを、ANOVAではF-distributionにおけるprobabilityを計算したのと同様、Chi-square testでもχ2のdistributionにおけるχ2のprobability (=p-value)を計算します。 […]
[…] Predictorが3群以上のカテゴリーであれば、連続変数であるoutcomeとの関係性はANOVAまたはKruscal-Wallis testで調べることができました。 […]
[…] なんかこの説明、聞いたことがありますね。そうです。3群以上で連続変数を比べた際に使った分散分析の時に出てきましたね。あの時使ったF-testと同じです。数式も同じになり、p-valueも同じとなります。 […]
[…] 連続変数の多群比較:ANOVAとKruskal-Wallis test:3群以上の比較で必要な、分散分析やF-scoreといった用語について解説します。 […]
[…] 連続変数を2群で比較する際、正規分布ならt-検定、そうでないならWilcoxonでしたね。連続変数を3群以上で比較する際、正規分布ならANOVA、そうでないならKruscal…でしたね。どうように、XとYが正規分布でないならPearsonではなく、Spearmanの相関係数を使います。 […]