相関係数

今回は、連続変数と連続変数の関係性を調べる方法の一つ、相関係数について解説いたします。

連続変数と連続変数の関係性

連続変数と連続変数の関係性を評価する方法としては、1) 散布図を描く、2) 相関係数（＋信頼区間、p-value）を求める、3) 線形回帰モデルを使う、という選択肢があります。ここでは、1)→2)を説明していきます。

散布図

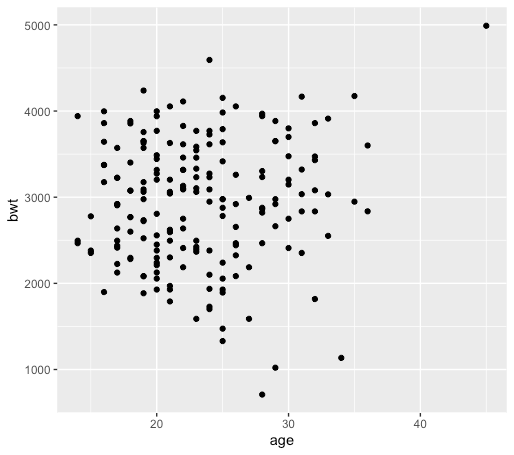
何はともあれ、まずは散布図を描きましょう。視覚的に捉えることは、データを数字で解析する前段階として非常に重要なステップです。

Rを使うなら、

dat_2%>% ggplot(aes(age, bwt))+
  geom_point()

によってscatter plotを描くことができます。

相関係数

連続変数同士に関連性があるかを調べるために、相関具合を表す相関係数と、関連性があるか否かを調べる検定を行います。検定の帰無仮説は、「両者に関連性はない」「両者は独立している」です。

ちなみに、causal inferenceにしても、prediction modelにしても、exposure (or predictor)とoutcomeという、用語の使い分けが存在し、研究の目的上この両者は逆であってはなりません。

しかし、この相関係数では、両者に区別は存在しません。すなわち、「AとBの相関係数」と「BとAの相関係数」は同じとなります。

Pearsonの相関係数

まず初めに、Pearsonの相関係数について説明します。ここでは、コレステロール（X）と年齢（Y）という、連続変数同士の相関をみてみましょう。

上のスライドの“r”や”ρ”が相関係数で、上記のような式で定義されます。この式の二行目（特に分子）に注目することよって、以下のことが理解できます。

「それぞれのデータのY（年齢）が期待値よりも大きいときに、X（コレステロール）が期待値よりも大きいという関係性」や「それぞれのデータのY（年齢）が期待値よりも小さいときに、X（コレステロール）が期待値よりも小さいという関係性」の場合は、相関係数は正となります。

「それぞれのデータのY（年齢）が期待値よりも小さいときに、X（コレステロール）が期待値よりも大きい関係性」や「それぞれのデータのY（年齢）が期待値よりも大きいときに、X（コレステロール）が期待値よりも小さい関係性」の時は、相関係数は負の値となります。

そして、両者に全く関係性がない場合は、相関係数は0となります。

これらは関係性を表す概念ですが、実際にはデータからその関係性を推測（計算）しなければなりません。

実際のデータから相関係数を推測（計算）

では、どのように相関係数を計算するのでしょうか。以下が、その計算式になります。

やはり分子に注目してください。データ上の期待値は平均値ですので、意味するところは、

ということです。

この「{X（コレステロール）と平均値の差}と{Y（年齢）と平均値の差}の積」が、正になるか負になるかは、スライドの右図のように4つの領域に分けることで理解できます。正と正の積、または負と負の積は、正になりますし、それ以外の積は負になりますね。

それぞれの患者でこの積を合計するため、正の領域に患者データが沢山あれば、相関係数は正となり、負の領域の患者のデータが沢山あれば、相関係数は負となります。そして、データが正と負の領域に混在すれば、合計することで正と負が相殺され0に近づいていきます。

一般的には、相関係数が0.7を超える、または-0.7未満であれば関係性が強いということができます。

Pearsonの相関係数の注意点

Pearsonの相関係数は、XとYで回帰直線を描いた際の、それぞれのデータがその直線にどのくらい近いかを示しているとも解釈することもできます。

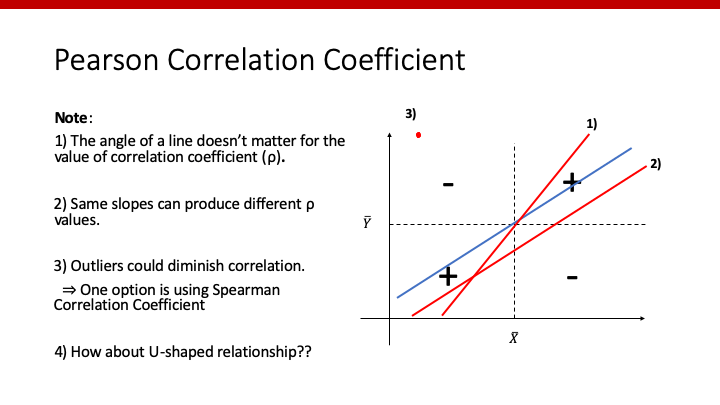
注意すべき点は、回帰直線の傾きが異なっていても、同じXとYの平均値を通る直線（上のスライドの1)の赤い線）でデータの線への近さが同じであれば、相関係数は同じになることです。

一方で、XとYの平均値を通らない直線となれば（上のスライドの2)の赤い線）、右下の「負」の領域にデータが多くあることを意味しているため、同じ傾きであっても相関係数は変化します。

また、3)のような外れ値が存在する場合、たった数個のデータであってもPearsonの相関係数に与える影響は大きいため、このような場合はSpearmanの相関係数を用いた方が良いでしょう。

前述のようにPearsonの相関係数は（回帰）直線に近いかを表しているため、正と負の領域を通るようなU-shapeの関係性には効力を発揮しません。明らかにU-shapeの関係性があったとしても、相関係数は0となることもあります。

検定と信頼区間

「関係性なし（相関係数0）」を帰無仮説とすることで、その相関係数となるprobability（→p-value）を求めることができます。T-scoreを計算し、T-distributionからそのprobabilityを計算します。t検定と一緒ですね。

ここで注意してほしいことが、相関係数は、サンプルサイズさえ大きければ簡単に有意差を出すことができる、ということです。仮に相関係数が0.1のとき、上のようにt-scoreを計算していくと、n=402とのきにt-scoreは2となります。（ざっくり言えば）t-scoreが2を超えてくるとp<0.05となるため、相関係数が0.1であってもp-valueは0.05未満となり、「統計学的有意」と言えてしまいます。

しかし、統計学的に有意であっても、相関係数が0.1である散布図をみればわかるように、XとYに殆ど関係性はみられません。このように、関係性を評価する際に、相関係数のp-valueを鵜呑みにするのは危険です。

実際のoutput

SASでは上のようなoutputがでてきます。前述のように、直線の傾きの情報はありません。

Rで相関係数と信頼区間を出してみましょう。

cor.test(dat_2$age, dat_2$bwt, method="pearson", conf.level=0.95)

とすれば、

##  Pearson's product-moment correlation
## 
## data:  dat_2$age and dat_2$bwt
## t = 1.2377, df = 187, p-value = 0.2174
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.05327129  0.22991649
## sample estimates:
##       cor 
## 0.0901444

と、相関係数だけでなく、p-valueや信頼区間も得ることができます。

Spearmanの相関係数

連続変数を2群で比較する際、正規分布ならt-検定、そうでないならWilcoxonでしたね。連続変数を3群以上で比較する際、正規分布ならANOVA、そうでないならKruscal-Wallisでしたね。どうように、XとYが正規分布でないならPearsonではなく、Spearmanの相関係数を使います。

その方法は、WilcoxonやKruscal-Wallisと同じです。データに順位づけ（ランキング）を行い、そのランキングの相関を調べるだけです。

Rのcodeは、

cor.test(dat_2$age, dat_2$bwt, method="spearman")

とすれば、

##  Spearman's rank correlation rho
## 
## data:  dat_2$age and dat_2$bwt
## S = 1056442, p-value = 0.4037
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##        rho 
## 0.06109078

というoutputがでてきます。

 

今回は連続変数通しの関係を調べる方法として、相関係数を解説しました。必ずscatter plotを描き、視覚的に確認することで、p-valueといった数字に惑わされないようにすることが大切ですね。

 

⇒医療従事者に必要な統計学と疫学（目次）へ

Reference

John Orav. BST 208: Stats for Med Research, Advanced. Introductory Statistics for Medical Research. Harvard T.H. Chan School of Public Health