正規分布とprobability

正規分布

今回は、正規分布を用いたprobabilityの計算についてです。p-valueも（帰無仮説における条件付き）probabilityであるので、後々のためにも理解が必要です。

正規分布とは

このnormal ( , )という表現、今後もよく出てきますので覚えておいてください。

正規分布といっても、そのcenter (mean)や広がり（standard deviation）によって様々です。しかし、それぞれのデータから平均値（μ）を引くことでそのセンターはゼロとなり、SD（σ）で割ることでその分布のSDは1となります。すなわち、normal (μ, SD)であったXの分布は、上記の計算によってnormal (1, 0)のstandard normalになる訳です。これをZ scoreと呼びます。

現実には我々は本当のSD（σ）を知ることができないため、自分の目の前にあるデータのSD（s）を使うしかありません。これをt-scoreと呼びます。

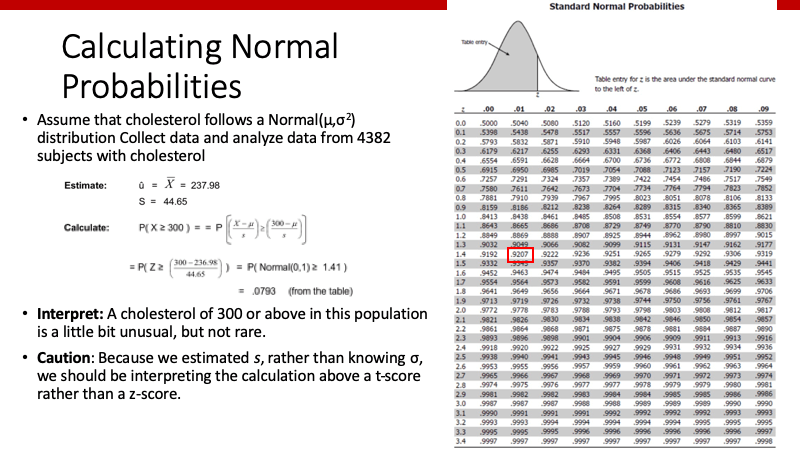
Z-scoreの使い方

このスライドでは、normal (0, 1)の分布をしたデータにおいて、X>=3となるprobabilityを考えています。このように、データが正規分布であった場合、その値またはそれより小さな値をとるprobability（下側確率）を、上のようなtableを用いたり、softwareを用いれば簡単にわかります。ちなみに、Rを使えば

> pnorm(3,mean=0,sd=1)
 0.9986501

となり、上のtableの赤枠と同じprobabilityとなります。

同様に、平均値とSDがわかっていれば、standard normalizationすることによって、その値の下側確率がわかります。

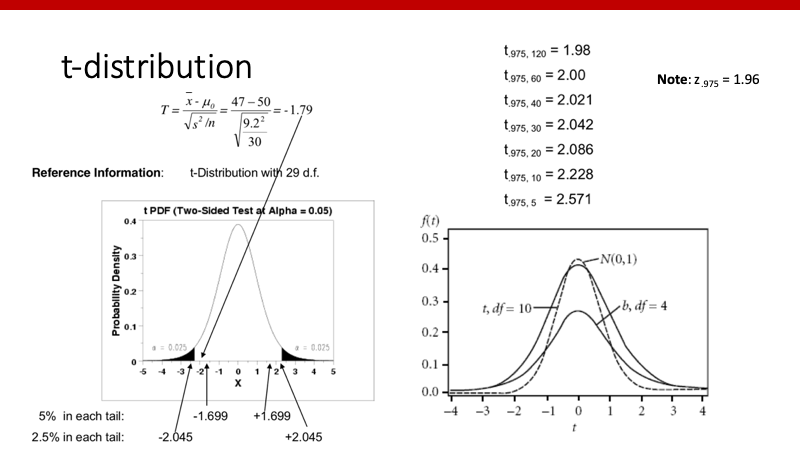
t-分布

Z-scoreを用いてprobabilityを計算する場合は上記のようにできますが、t-scoreを用いたprobabilityは若干異なります。下記の図はy軸にprobabilityをとっていますが、それぞれの曲線はdegree of freedomによって少しずつ異なります。dfが大きければ大きいほど、それぞれのprobabilityはZ-scoreの場合に近づきます。97.5%のデータが左側にくる値Z_0.975は1.96でしたが、dfが小さければこの値は大きくなります。sample sizeが小さいと、同じprobabilityを出すためにより極端な値が必要ということですね。

⇒医療従事者に必要な統計学と疫学（目次）へ

Reference