交絡因子（confounder）

今回は、交絡因子（confounder）の話です。研究に携わる医師、疫学者、統計学者、データサイエンティストなど、様々な職種の方々が使う用語ですが、実はその定義、使う人によって異なります。

はじめに

交絡因子（confounder）の定義としては

疫学者 vs. 統計学者・データサイエンティスト

といった構図になります。

ただし、疫学者と統計学者は共に公衆衛生学教室で同じ医学論文を書いていることも多いので、互いの定義の違いを理解して話をすることができます。しかし、データサイエンティストは統計学の一種のような学問をしているものの、公衆衛生学とは全く異なる学部であることも多く、普段は疫学者と一緒に仕事をしていません。そのため、いざ同じチームで話をした時に、全く話が噛み合わないことが多々あります。

ここではまず、統計学者やデータサイエンティストが使う交絡因子の定義を解説した後、その定義をなぜ疫学者が嫌うのかについて、解説したいと思います。

“Change in estimate” definition

例えば、曝露因子（A）とアウトカム（Y）の関係性を見つけたいとしましょう。この関係性の大きさが”estimate”であり、「Aが変化した際のYの変化の大きさ」のことです。

統計学者やデータサイエンティストは、第三の因子（L）を考慮する前と後で、このestimateが変化するのであれば、この第三の因子がconfounderであると定義しています。すなわち、データのみからconfounderかどうか判断します。

具体的には、

と呼びます。

上のスライドは、母親の妊娠中のsmoking (A)と子供のBirth weight (Y)との関連を調べようとした際、妊娠中のアルコール摂取（L）が交絡因子であるかどうかを調べようとしたものです。

Lで調節する前のAとYの関係性の大きさは、linear regression modelではβで示すことができます。この場合、喫煙者（smoke=1）は非喫煙者（smoke=0）と比べて子供のbirth weightが200g小さいということを意味しています。

一方、アルコールをmodelに入れることで、アルコールで調節（adjust）すると、喫煙者（smoke=1）は非喫煙者（smoke=0）と比べてbirth weightが150g小さいという関係性に変化しました。

この変化率: (200-150)/200=25%が10% (または20%)を超えているので、アルコール摂取は喫煙とbirth weightの関係のconfounderである、といいます。

この定義はかなりpopularですが、因果推論をする際には間違いを引き起こすことがあるので注意が必要です。DAGを使って説明しますので、DAGをご存知ない方は、記事「因果推論とDAG」を参照してください。

まずは、この定義であっても問題ない例から見ていきましょう。

“Change in estimate”で問題ない例

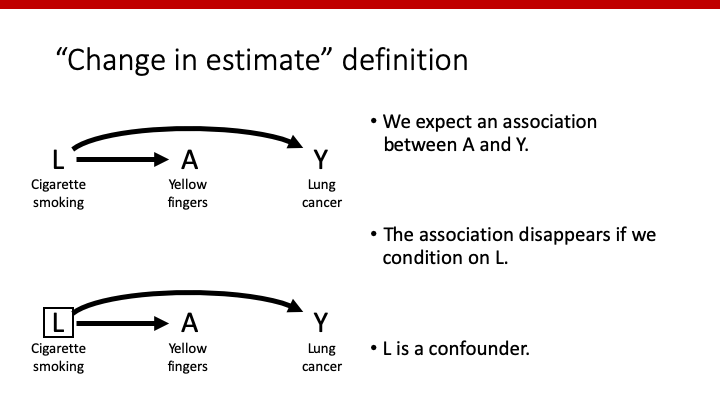
ここでは、喫煙によって指が黄色くなり、喫煙によって肺癌が引き起こされていますが、黄色い指が肺癌を引き起こしている訳ではない、という状況です。この場合、喫煙をmodelに入れなければ黄色い指と肺癌の間に関連ありというbiasとなってしまうため、biasを取り除くためには喫煙はadjustしなければならない因子、すなわちconfounderであるはずです。

では、喫煙がconfounderであるかどうかの判断に、“Change in estimate” definitionを使ってみましょう。Adjust前のAとYは関連ありですが、adjust後のAとYは関連無しとなっています。従って、L（喫煙）はconfounderであることになり、問題ありません。

では次に、上記の定義では問題が起こる例をみていきます。

“Change in estimate”で問題のある例

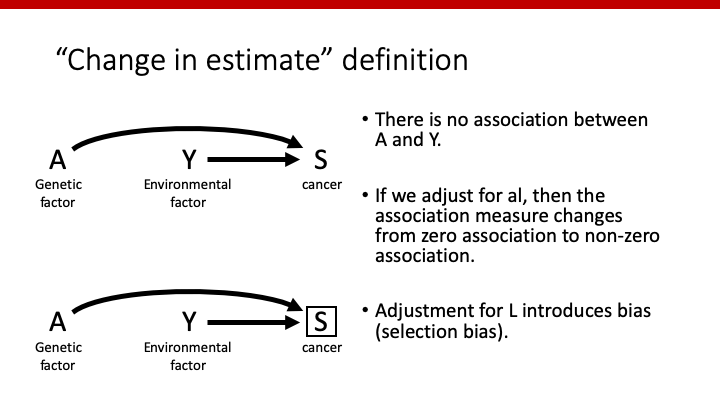
因果推論においては、このようなS（癌）はcolliderであるため、AがYに影響を与えているか調べるためにはSで条件付けしてはいけません（わからない人は、こちらを見てください！）。Sはcolliderであって、confounderではありません。

しかし、“Change in estimate” definitionを使ってみると、adjust前のAとYは関連なしですが、adjust後のAとYは関連ありとなっています。“Change in estimate” definitionを使うと、このSはconfounderと判断され、モデルに入れた方が良いという結論に至ってしまいます。繰り返しますが、Sはconfounderではなくcolliderのため、モデルに入れて調節してはなりません。もしモデルに入れてしまうと、因果推論が間違った方向に向かってしまいます。

Structured approach

では、どうすれば良いのでしょうか。この“Change in estimate” definitionがnon-structured approachの一つと捉えられるのに対し、structured approachというもう一つの方法があります。この方法、confounderを見つけるために、DAGしか使いません。考えることは2つだけです。

たったこれだけです。

では先ほどの例を考えてみましょう。

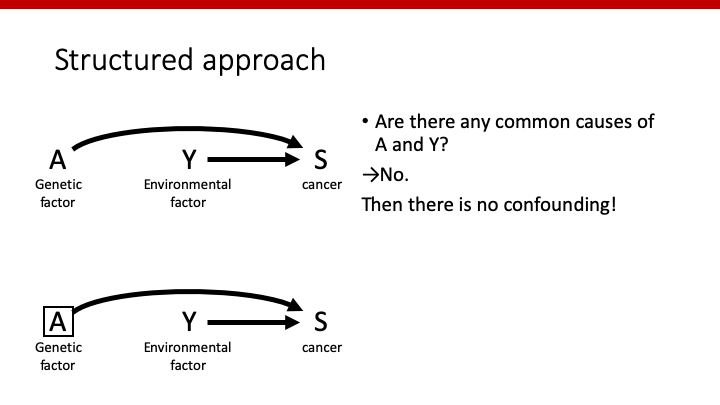
このDAGにおいて、癌はAとYの共通する原因ではありませんよね？すなわち、「Sはconfounderではない」、たったそれだけです。

このように、因果推論をする上では、“Change in estimate” definitionではなく、Structured approachを使うべきです。

おわりに

いかがでしたか。因果推論における疫学者のconfounderの考え方と、data drivenな統計学者・データサイエンティストのconfounderの考え方の違い、ご理解いただけたでしょうか。研究もチームで立ち向かう必要が増えてきた今日において、彼らが一つのチームに共存することもありえます。是非、このような差を理解した上で議論できれば良いですね。

 

⇒医療従事者に必要な統計学と疫学（目次）へ

Reference