線形回帰分析〜その2：最小二乗法

Linear regressionの基礎、読んでいただけたでしょうか。そちらを読めば、modelの数式の意味が理解できたと思います。

今度は、どのように直線の切片や係数を求めるのか、そして、どのようにそれが有意かどうか判断するのか、その理論を解説していきます。今回もpredictorが一つだけのsimple linear regressionを用いて説明します。

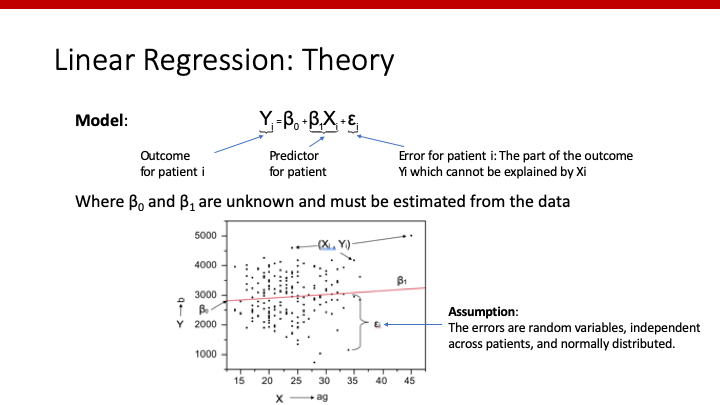
前回は、皆さんがお馴染みの数式としてわかりやすくするため、切片（intercept）をa、predictor 1の係数（slope）をb、というようにしていましたが、predictorやcovariateの数が増えると、どのアルファベットが、どのpredictor/covariateの係数なのか、わかりにくくなります。

そこで今後は、切片（intercept）をβ₀、predictor 1の係数（slope）をβ₁、predictor 2の係数をβ₂、というように表現します。

やりたいこと（linear regression modelで知りたい値）は、以下の通りです。

ちなみに、βなどアルファベットの上に” ̂”が付く場合、”ハット”と呼びます。“β^₁“は自分たちが持っているデータ（サンプル）から導き出したmodelのslopeであり、whole populationの本物のslopeである”β₁“とは区別して表現します。

βsを推定：Least Squares Estimation

どのように、β₀やβ₁を求めればよいのでしょうか。目的は、自分たちが持っているデータ全体を最もよく表してくれる直線をさがすことです。

では、「最もよく表してくれる」とはどういうことでしょうか。数学的には、個々の患者のoutcomeである”Yi”と、modelから推測されたoutcomeである”β₀+β₁*Xi”の差が、全体として最も小さくなる場合、ということができます。すなわち、個々の患者でその差を計算し、（プラスとマイナスで相殺されないために）二乗し、全ての患者で足し合わせたもの（Σ）、それを最小にする、そのようなβ₀やβ₁を探す必要があります。これが、Least Squares Estimation（最小二乗法）です。

全てのβ₀やβ₁の組み合わせを試して比べる方法もあるかもしれませんが、実際はsoftwareがスライドのような計算式でβ^₀やβ^₁を求めています。

Residuals and Variances

先ほど説明した「個々の患者のoutcomeである”Yi”と、modelから推測されたoutcomeである”β₀+β₁*Xi”の差」というものが、residualと呼ばれます。二乗したものを全ての患者で足し合わせ、平均化したものがMean Squared Error (MSE)と呼ばれ、modelの良さ（fitting）の指標となります。

β^₁のvarianceも求めなければなりません。なぜなら、varianceからstandard errorが計算でき、それによりβ^₁のt-scoreの計算と検定が可能となります。また、standard errorは信頼区間の計算にも必要になります。

検定

帰無仮説はβ₁=0です。そして、先ほど計算したβ^₁

やβ^₁のstandard errorから、t-scoreを計算します。t-scoreからprobability（p-value）の算出方法がわからない人はこちらを参照してください。

信頼区間

そして最後に、β^₁とβ^₁のstandard errorを用いて、信頼区間を計算します。

まとめ

今回は、linear regression modelの数式内にある数字（βs）やその検定方法を説明しました。説明した数字全て、softwareで自動的にoutputされますのでご安心してください。

例えば、df_bwというdata frameにおいて、outcomeをbwt、predictorをlwtとした場合のlinear regressionでは、lm()を使って以下のようになります。

model<-lm(bwt~lwt, data=df_bw)
summary(model)

## Call:
## lm(formula = bwt ~ lwt, data = df_bw)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2192.14  -503.69    -4.03   508.42  2075.53 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 2367.767    228.414  10.366   <2e-16 ***
## lwt            4.445      1.713   2.595   0.0102 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 718.2 on 187 degrees of freedom
## Multiple R-squared:  0.03476,    Adjusted R-squared:  0.02959 
## F-statistic: 6.733 on 1 and 187 DF,  p-value: 0.01021

といった感じです。

bwt=2367.767 + 4.445*lwt

というmodelができました。このoutputから、β^₁=4.445であり、そのstandard errorが1.713、t-scoreが2.595、p-valueが0.0102ということがわかります。

⇒医療従事者に必要な統計学と疫学（目次）へ

Reference