線形回帰分析〜その5：必要な変数、不要な変数

因果推論におけるregression modelの作るには、どのような変数をmodelに入れ、どのような因子をmodelから外さなければならないのかを、知る必要があります。今回は、それぞれ入れるべき変数、外すべき変数について解説していきます。

因果推論ですので、X₁のYに対する影響を知りたい場合の、第2の変数X₂をmodelに入れるべきかどうか考えます。

Confounder（交絡因子）

統計学的には、predictor (X₁)と関係しており、かつoutcome (Y)に独立して関連しているものをconfounderと定義します（上の図のような関係）。そのため、confounderをmodelに加える（adjustする）前後でX₁のとYの関係性が変化する、すなわち係数β₁が変化します（詳細はこちらを参照してください）。変化率のカットオフとしては、10%や20%がよく使われます。

因果推論をする上では、confounderを考慮しないと本来の「X₁のYに対する影響」を間違って評価（→bias）してしまうため、confounderで”adjust（調整）”する必要があります。すなわち、Regression modelにconfounderを入れるべきです。

Example

喫煙（X₁：smoke）の出生児体重（Y：bwt）に対する影響を調べたいとします。

# Crude
lm(bwt~smoke,data=df_bw)%>% summary()

## Call:
## lm(formula = bwt ~ smoke, data = df_bw)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2064.51  -477.51    35.04   545.04  1935.04 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3054.96      66.94  45.638  < 2e-16 ***
## smoke1       -281.44     106.98  -2.631  0.00923 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 717.8 on 187 degrees of freedom
## Multiple R-squared:  0.03569,    Adjusted R-squared:  0.03053 
## F-statistic: 6.921 on 1 and 187 DF,  p-value: 0.009228

そして、X₂：人種（race）がconfounderかどうかcheckしてみましょう。

# Adjusting for race
lm(bwt~smoke+race,data=df_bw)%>% summary()

## Call:
## lm(formula = bwt ~ smoke + race, data = df_bw)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2314.23  -442.24    36.08   491.77  1654.77 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3335.23      91.75  36.350  < 2e-16 ***
## smoke1       -426.99     109.01  -3.917 0.000126 ***
## race2        -451.31     153.08  -2.948 0.003609 ** 
## race3        -454.74     116.45  -3.905 0.000132 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 688.1 on 185 degrees of freedom
## Multiple R-squared:  0.1235, Adjusted R-squared:  0.1093 
## F-statistic: 8.688 on 3 and 185 DF,  p-value: 2.012e-05

β₁の変化が -281-(-427)/281 = 52%となり、10% (or 20%)を上回っています。この場合、統計学的には、人種は喫煙と出生児体重の関係をconfoundするもの、というように定義されます。よって、raceはmodelに入れましょう。

Intermediary Variable（介在因子）

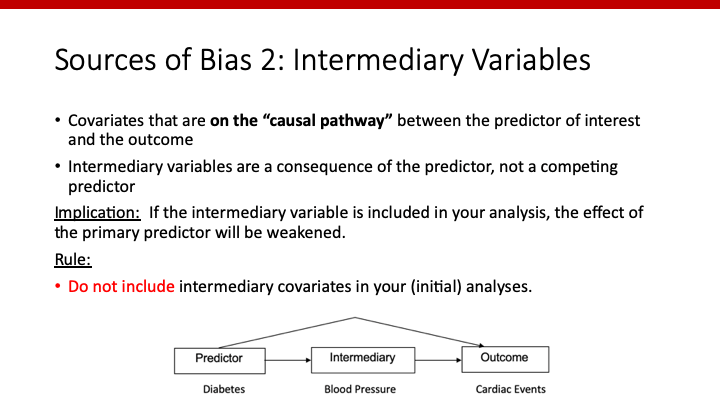
DAGで説明したように、causal pathway上にあるintermediate variableで調整した場合、本来評価したい「X₁のYに対する影響」が過小評価されてしまいます。

そのため、Modelにintermediate variableは入れるべきではありません。

Effect Modifier

Effect modifierとは、「X₁のYに対する影響」を変化させる因子のことです。この場合、effect modifierで層化（stratification）して判断するんでしたね（こちらの記事を参照）。

Regressionでは、“interaction term”というものをmodelに入れることで、その有無を判断できます。Interaction termに関しては、別に記事にします。

Collinear Covariate

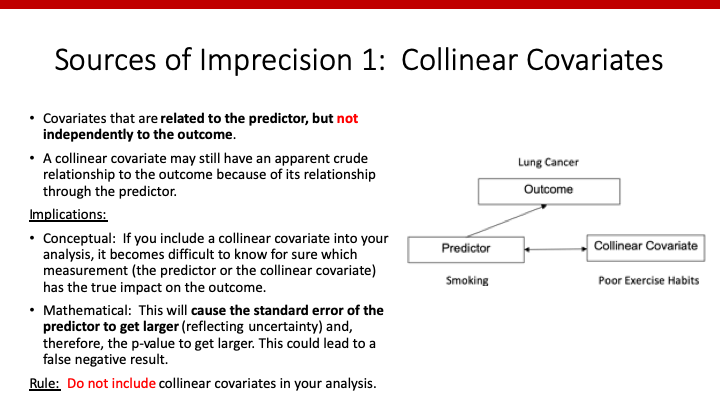
X₂がX₁と関係しており、Yとは関連していない場合、X₂は”collinear variable“と呼ばれます（collinearity: 共線性）。

この場合、X₁とX₂の両方がをmodelに入れてしまうと、どちらがYに影響を持っているのか判断できなくなります。

また、前回説明したように、collinear variableをmodelに加えることによってβ₁のvarianceは大きくなってしまい、検出力が小さくなります（こちらも変化率のカットオフとして、10%がよく使われます）。

以上のような理由から、collinear variableはmodelに含めないようにしなければなりません。

Example

Confounderの時と同じく、喫煙（X₁：smoke）の出生児体重（Y：bwt）に対する影響を調べたいとします。Crude analysisも前回と一緒です。今回は、uiがcollinear covariateかどうか調べてみましょう。

# Adjusting for ui
lm(bwt~smoke+ui,data=df_bw)%>% summary()

## Call:
## lm(formula = bwt ~ smoke + ui, data = df_bw)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1797.79  -461.62    47.21   501.21  1862.21 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3127.79      67.09  46.621  < 2e-16 ***
## smoke1       -256.18     103.26  -2.481 0.013991 *  
## ui1          -558.43     141.87  -3.936 0.000117 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 691.5 on 186 degrees of freedom
## Multiple R-squared:  0.1098, Adjusted R-squared:  0.1003 
## F-statistic: 11.48 on 2 and 186 DF,  p-value: 1.998e-05

β₁のstandard errorの変化は、103-107/107 = – 4%と下がっていますね。したがって、uiはcollinear covariateではない、と判断されます。

Significant Predictor

X₂がX₁と関係しておらず、Yのみと関連している場合、X₂はYを予測する上で非常に大切な変数になりますね。これを、とても大事な予測変数という意味を込めてsignificant predictorと呼びます。

そして、X₂がsignificant predictorであれば、Yのみにと関連しているため、上述のようにX₂をmodelに加えることによってβ₁のvarianceが小さくなり、検出力が上がります。よって、collinear variableはmodelに含めるべきです。

※Significant predictorの定義としてβ₁のvarianceの上昇率を使う方法もあると思いますが、p-valueを使って判断することも多いようです。

Example

今回は、htがsignificant predictorかどうか調べてみましょう。

# Adjusting for ui
lm(bwt~smoke+ht,data=df_bw)%>% summary()

## Call:
## lm(formula = bwt ~ smoke + ht, data = df_bw)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2093.45  -449.45    22.98   518.55  1908.98 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3081.02      67.64  45.547  < 2e-16 ***
## smoke1       -278.57     106.12  -2.625  0.00938 ** 
## ht1          -428.20     212.42  -2.016  0.04526 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 712 on 186 degrees of freedom
## Multiple R-squared:  0.05631,    Adjusted R-squared:  0.04616 
## F-statistic: 5.549 on 2 and 186 DF,  p-value: 0.004563

htのp-value = 0.045と有意であり、htはsignificant predictorでありmodelに加えるべき、ということがわかります。

関係のないvariable

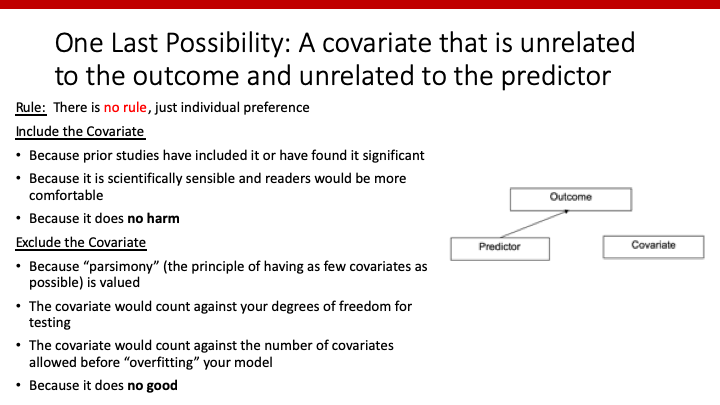
X₂がX₁にもYにも関連のない場合は、どうしたら良いのでしょうか。この場合、X₂をmodelに入れても害もなければメリットもないため、特にルールはありません。

変数の選び方のまとめ

X₁のYに対する影響を考える（因果推論）をする際、別の変数X₂をmodelに入れるべきか否か、まとめますと

ということになりますね。

実際の例

最後に、これまで勉強した事を元に、それぞれの変数をmodelに入れるかどうか考えてみましょう。

この例では、妊娠中の喫煙（exposure / predictor）が出生児体重（outcome）にどのような影響を与えるのかを調べています。ですので、必ずmodelにsmokeが入っています。

lm(bwt~smoke+X2, data=df_bw)%>%summary()

このX₂をmodelに入れた場合のβ₁やそのstandard errorの変化率をまとめたのものが、上記の表です。

Confoundingを、それぞれの因子を加えることによってβ1（smokingの係数）が10%以上変化するもの、と定義するのであれば、”Race”と”Any PTL”がconfounderとなり、modelに入れるべき因子となります。

Collinear variableを、β1のstandard errorが10%以上増加したものと定義するのであれば、今回のデータセットには、smokingとのcollinear variableはないと判断できます。

Significant predictorの定義としてβ1のstandard errorを使っても良いですが、今回は（outcomeに有意に関連している、という意味で）p-valueを使いました。すると、”LWT”, “Race”, “Any PTL”, “Hypertension”, “UI”がsignificant predictorとなり、modelに入れるべき変数となります。

以上より、final modelとしては、

lm(bwt~smoke+race+ptl+low+ht+ui, data=df_bw)%>%summary()

となります。

さいごに

いかがでしたでしょうか。因果推論では、持っているデータ全てをmodelに入れることが良いことではありません。それぞれの因子について、入れるべきかどうか判断しなければなりません。今回は、2つ目の変数をmodelに入れるべきかの判断を、統計学的に考える方法を解説しました。

 

⇒医療従事者に必要な統計学と疫学（目次）へ

 

Reference

John Orav. BST 213: Applied Regression for Clinical Research. Harvard T.H. Chan School of Public Health