線形回帰分析〜その3：ANOVA

前回は、linear regressionのβの求め方やその検定方法について解説しました。直線のslopeである個々の係数βが知りたい値であり、それぞれのβが有意か否か検定（test）するんでしたね。

しかし、linear regressionにはもう一つのアプローチ方法があります。知りたい事は「そのmodelは全体としてどのくらいデータにfitしているか」であり、そのfit具合を検定（test）する、というものです。今回は、その方法である”ANOVA“について、解説したいと思います。

三つの分散

ANalysis Of VAriance (ANOVA)というだけあって、分散を元に解析していきます。そして、理解すべき三つの分散が存在します。

以上をもっとわかりやすくした図が、以下の図です。青い丸が個々のデータ（Yi）、斜めの黒い線がlinear regression model（Y^）、水平の黒い直線が只の平均値（Y_bar）です。

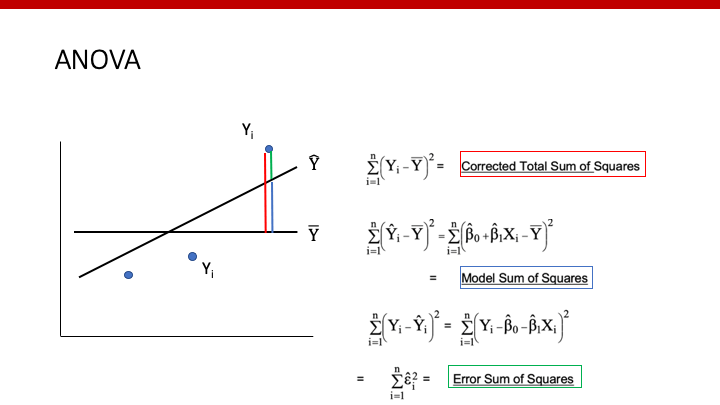
上の図の赤い線が、全てのvariance（1）になります。そして、そのvarianceは、modelで説明できるvariance（青：2）と説明できないvariance（緑：3）の合計であることがわかります。

別の図を使って、理解を深めましょう。

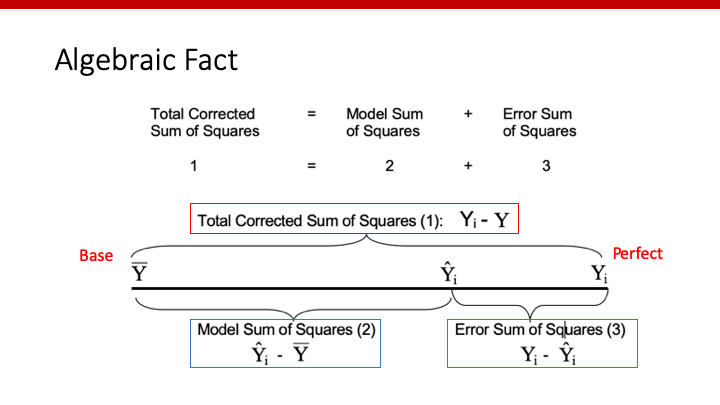
やはり、Total Sum of Squares (TSS)は、Model Sum of Squares (MSS)とError Sum of Squares (ESS)の合計であることがわかります。

TSSは変わりませんが、modelが良くなればなるほどY^iが右にずれますので、MSSが大きくなり、ESSが小さくなります。

Modelはどの程度データへfitしているのか

r-square

自分のlinear regression modelが、そのデータにどの程度fitしている（どの程度良く表している）のでしょうか。その指標として用いられるのがr²（r-square）です。上記のTSSにおけるMSSの割合を表していますので、高ければ高いほどmodelは良いことになりますね。そして、図からわかるように、r²のとりうる範囲は0（modelは全然よくない）~1（modelはperfect）となります。

注意すべき点は、modelの中にpredictorやcovariateを加えれば加えるほど、少しずつでも常にr²は増加してしまうことです。そのため、r²を指標にpredictorやcovariateの選択を考えてしまうと、どんなに役立たないvariableであってもmodelに入れた方がよい、という間違ったことになってしまいます。

Adjusted r-square

この問題を解決するために使うのが、adjusted r²です。上のスライドにある式をご覧になったらわかるように、predictorやcovariateの数（parameterの数）が分母にありますので、variableを加えた際のr²の増加に対するpenaltyとして作用します。

r²とadjusted r²の使い分け

では、どのようにこの二者を使い分けるのでしょうか。

通常、ある一つのmodelがどの程度データにfitしているかの指標が欲しい場合は、r²を用いますし、論文などでもr²を提示します。

一方、predictorの選択時、modelに入れるかどうか悩んでいる際には、adjusted r²を使います。有用なpredictorでれば、adjusted r²は上昇しますが、無用なpredictorであればadjusted r²は低下するからです。

データへのfit具合を検定

統計学なので、modelのデータへのfitの”程度”だけでなく、それが”有意かどうかの検定”が欲しいですよね。

ここで用いるのは、F-testという検定です。分子にMSS、分母にESSを置くことで、両者の分散を比較していることになります。良いmodelである方がMSSが大きくなりESSが小さくなるため、F-scoreは大きくなります。このF-scoreの、F-distributionにおけるprobability、それがp-valueです。

なんかこの説明、聞いたことがありますね。そうです。3群以上で連続変数を比べた際に使った分散分析の時に出てきましたね。あの時使ったF-testと同じです。数式も同じになり、p-valueも同じとなります。

Rで解析

最後に、rを使ってANOVAを行ってみましょう。

df_bwというdata frameで、outcomeをbwt、predictorをlwtとしてlinear regression modelを作りました。anova()で今回勉強したvarianceを知ることができます。

lm(bwt~lwt,data=df_bw)%>%anova()

## Analysis of Variance Table
## 
## Response: bwt
##            Df   Sum Sq Mean Sq F value  Pr(>F)  
## lwt         1  3473052 3473052  6.7334 0.01021 *
## Residuals 187 96454213  515798                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

上のoutputで、MSSが3473052、ESSが96454213です。従って、r-squareは

3473052/(3473052+96454213) = 0.03476

となります。たったの3.5%しかmodelは全体のvarianceを説明できていないんですね。

このように手計算しなくても、もちろんcodingだけでr-squareをoutputする方法があります。

lm(bwt~lwt,data=df_bw)%>%summary()

## Call:
## lm(formula = bwt ~ lwt, data = df_bw)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2192.14  -503.69    -4.03   508.42  2075.53 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 2367.767    228.414  10.366   <2e-16 ***
## lwt            4.445      1.713   2.595   0.0102 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 718.2 on 187 degrees of freedom
## Multiple R-squared:  0.03476,    Adjusted R-squared:  0.02959 
## F-statistic: 6.733 on 1 and 187 DF,  p-value: 0.01021

r-squareだけでなく、adjusted r-square、F-score、そしてそこから計算したp-valueも載っていますね。

Adjusted r-squareが（0から）0.0259に増加しているためlwtは加えるべきpredictorなんでしょう。そして、F-testのp-valueが0.01021であるため、このmodelはpredictorのない場合よりも、有意に良いモデルであると判断できます。

まとめ

前回は、linear regression model中のそれぞれの係数の求め方や検定について説明しました。今回は、そのmodelがどの程度データにfitしているのかについて解説しました。少しずつ、線形回帰分析への理解が深まってきましたか？

⇒医療従事者に必要な統計学と疫学（目次）へ

Reference